triangulation

Contents

triangulation#

graph_tool.generation.triangulation(points, type='simple', periodic=False)[source]#

Generate a 2D or 3D triangulation graph from a given point set.

Parameters:
pointsnumpy.ndarray

Point set for the triangulation. It may be either a N x d array, where N is the number of points, and d is the space dimension (either 2 or 3).

typestring (optional, default: 'simple')

Type of triangulation. May be either ‘simple’ or ‘delaunay’.

periodicbool (optional, default: False)

If True, periodic boundary conditions will be used. This is parameter is valid only for type=”delaunay”, and is otherwise ignored.

Returns:
triangulation_graphGraph

The generated graph.

posVertexPropertyMap

Vertex property map with the Cartesian coordinates.

See also

random_graph

random graph generation

Notes

A triangulation [cgal-triang] is a division of the convex hull of a point set into triangles, using only that set as triangle vertices.

In simple triangulations (type=”simple”), the insertion of a point is done by locating a face that contains the point, and splitting this face into three new faces (the order of insertion is therefore important). If the point falls outside the convex hull, the triangulation is restored by flips. Apart from the location, insertion takes a time O(1). This bound is only an amortized bound for points located outside the convex hull.

Delaunay triangulations (type=”delaunay”) have the specific empty sphere property, that is, the circumscribing sphere of each cell of such a triangulation does not contain any other vertex of the triangulation in its interior. These triangulations are uniquely defined except in degenerate cases where five points are co-spherical. Note however that the CGAL implementation computes a unique triangulation even in these cases.

References

Examples

>>> points = random((500, 2)) * 4
>>> g, pos = gt.triangulation(points)
>>> weight = g.new_edge_property("double") # Edge weights corresponding to
...                                        # Euclidean distances
>>> for e in g.edges():
...    weight[e] = sqrt(sum((array(pos[e.source()]) -
...                          array(pos[e.target()]))**2))
>>> b = gt.betweenness(g, weight=weight)
>>> b[1].a *= 100
>>> gt.graph_draw(g, pos=pos, vertex_fill_color=b[0],
...               edge_pen_width=b[1], output="triang.pdf")
<...>

>>> g, pos = gt.triangulation(points, type="delaunay")
>>> weight = g.new_edge_property("double")
>>> for e in g.edges():
...    weight[e] = sqrt(sum((array(pos[e.source()]) -
...                          array(pos[e.target()]))**2))
>>> b = gt.betweenness(g, weight=weight)
>>> b[1].a *= 120
>>> gt.graph_draw(g, pos=pos, vertex_fill_color=b[0],
...               edge_pen_width=b[1], output="triang-delaunay.pdf")
<...>

2D triangulation of random points:

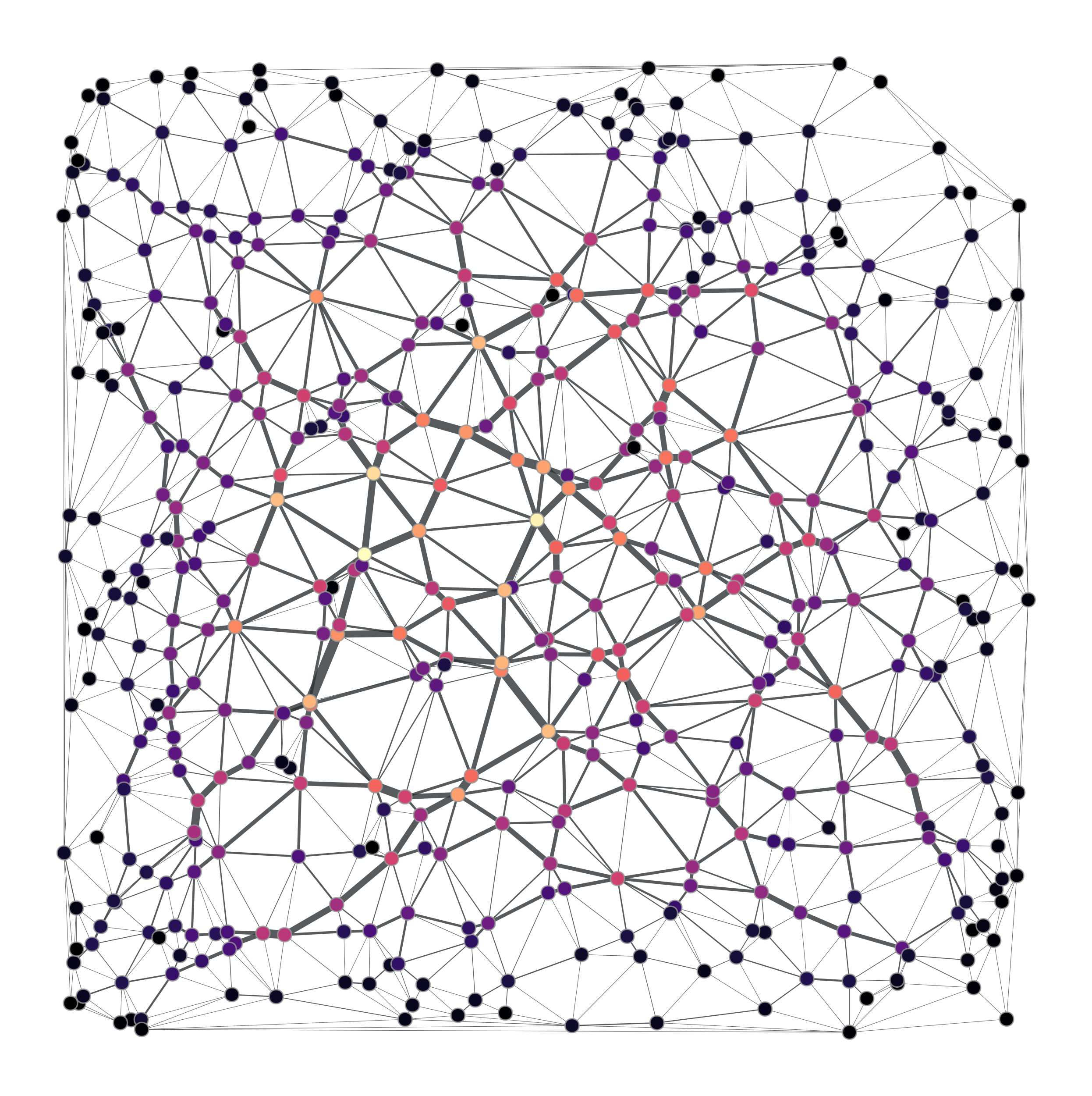
../_images/triang.png ../_images/triang-delaunay.png

Left: Simple triangulation. Right: Delaunay triangulation. The vertex colors and the edge thickness correspond to the weighted betweenness centrality.

Contents