min_st_cut

Contents

min_st_cut#

graph_tool.flow.min_st_cut(g, source, capacity, residual)[source]#

Get the minimum source-target cut, given the residual capacity of the edges.

Parameters:
gGraph

Graph to be used.

sourceVertex

The source vertex.

capacityEdgePropertyMap

Edge property map with the edge capacities.

residualEdgePropertyMap

Edge property map with the residual capacities (capacity - flow).

Returns:
partitionEdgePropertyMap

Boolean-valued vertex property map with the cut partition. Vertices with value True belong to the source side of the cut.

Notes

The source-side of the cut set is obtained by following all vertices which are reachable from the source in the residual graph (i.e. via edges with nonzero residual capacity, and reversed edges with nonzero flow).

This algorithm runs in \(O(V+E)\) time.

References

Examples

>>> g = gt.load_graph("mincut-st-example.xml.gz")
>>> cap = g.edge_properties["weight"]
>>> src, tgt = g.vertex(0), g.vertex(7)
>>> res = gt.boykov_kolmogorov_max_flow(g, src, tgt, cap)
>>> part = gt.min_st_cut(g, src, cap, res)
>>> mc = sum([cap[e] - res[e] for e in g.edges() if part[e.source()] != part[e.target()]])
>>> print(mc)
3
>>> pos = g.vertex_properties["pos"]
>>> res.a = cap.a - res.a  # the actual flow
>>> gt.graph_draw(g, pos=pos, edge_pen_width=gt.prop_to_size(cap, mi=3, ma=10, power=1),
...               edge_text=res, vertex_fill_color=part, vertex_text=g.vertex_index,
...               vertex_font_size=18, edge_font_size=18, output="example-min-st-cut.pdf")
<...>
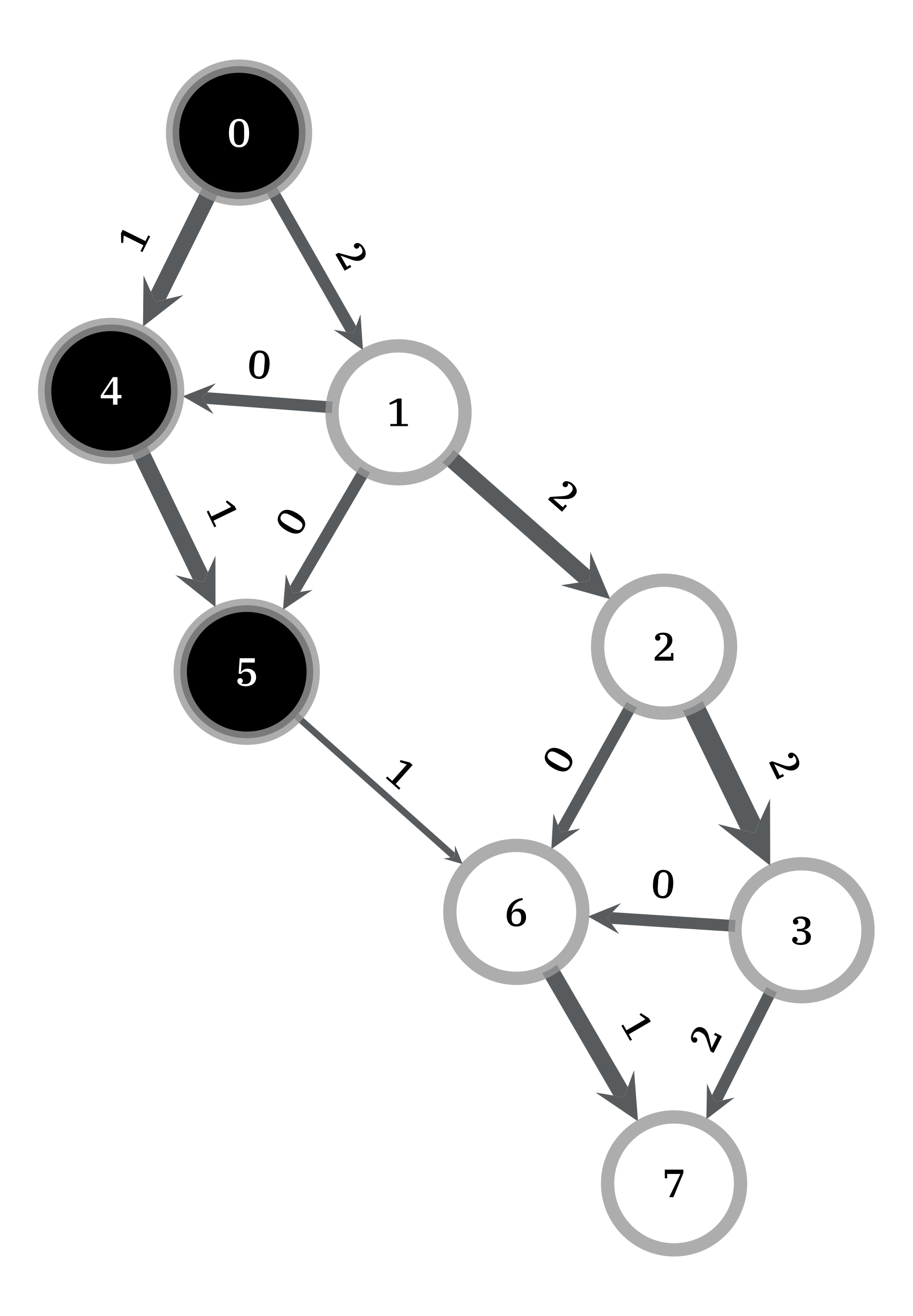
../_images/example-min-st-cut.png

Edge flows obtained with the Boykov-Kolmogorov algorithm. The source and target are labeled 0 and 7, respectively. The edge capacities are represented by the edge width, and the maximum flow by the edge labels. Vertices of the same color are on the same side the minimum cut.#

Contents