trust_transitivity

graph_tool.centrality.trust_transitivity(g, trust_map, source=None, target=None, vprop=None)

Calculate the pervasive trust transitivity between chosen (or all) vertices in the graph.

Parameters:

gGraph

Graph to be used.

trust_mapEdgePropertyMap

Edge property map with the values of trust associated with each edge. The values must lie in the range [0,1].

sourceVertex (optional, default: None)

Source vertex. All trust values are computed relative to this vertex. If left unspecified, the trust values for all sources are computed.

targetVertex (optional, default: None)

The only target for which the trust value will be calculated. If left unspecified, the trust values for all targets are computed.

vpropVertexPropertyMap (optional, default: None)

A vertex property map where the values of transitive trust must be stored.

Returns:

trust_transitivityVertexPropertyMap or float

A vertex vector property map containing, for each source vertex, a vector with the trust values for the other vertices. If only one of source or target is specified, this will be a single-valued vertex property map containing the trust vector from/to the source/target vertex to/from the rest of the network. If both source and target are specified, the result is a single float, with the corresponding trust value for the target.

See also

eigentrust

eigentrust centrality

betweenness

betweenness centrality

pagerank

PageRank centrality

Notes

The pervasive trust transitivity between vertices i and j is defined as

\[t_{ij} = \frac{\sum_m A_{m,j} w^2_{G\setminus\{j\}}(i\to m)c_{m,j}} {\sum_m A_{m,j} w_{G\setminus\{j\}}(i\to m)}\]

where \(A_{ij}\) is the adjacency matrix, \(c_{ij}\) is the direct trust from i to j, and \(w_G(i\to j)\) is the weight of the path with maximum weight from i to j, computed as

\[w_G(i\to j) = \prod_{e\in i\to j} c_e.\]

The algorithm measures the transitive trust by finding the paths with maximum weight, using Dijkstra’s algorithm, to all in-neighbors of a given target. This search needs to be performed repeatedly for every target, since it needs to be removed from the graph first. For each given source, the resulting complexity is therefore \(O(V^2\log V)\) for all targets, and \(O(V\log V)\) for a single target. For a given target, the complexity for obtaining the trust from all given sources is \(O(kV\log V)\), where \(k\) is the in-degree of the target. Thus, the complexity for obtaining the complete trust matrix is \(O(EV\log V)\), where \(E\) is the number of edges in the network.

Parallel implementation.

If enabled during compilation, this algorithm will run in parallel using OpenMP. See the parallel algorithms section for information about how to control several aspects of parallelization.

References

[richters-trust-2010]

Oliver Richters and Tiago P. Peixoto, “Trust Transitivity in Social Networks,” PLoS ONE 6, no. 4: e1838 (2011), DOI: 10.1371/journal.pone.0018384 [sci-hub, @tor]

[adamic-polblogs]

L. A. Adamic and N. Glance, “The political blogosphere and the 2004 US Election”, in Proceedings of the WWW-2005 Workshop on the Weblogging Ecosystem (2005). DOI: 10.1145/1134271.1134277 [sci-hub, @tor]

Examples

>>> g = gt.collection.data["polblogs"]
>>> g = gt.GraphView(g, vfilt=gt.label_largest_component(g))
>>> g = gt.Graph(g, prune=True)
>>> w = g.new_edge_property("double")
>>> w.a = np.random.random(len(w.a))
>>> t = gt.trust_transitivity(g, w, source=g.vertex(42))
>>> gt.graph_draw(g, pos=g.vp["pos"], vertex_fill_color=t,
...               vertex_size=gt.prop_to_size(t, mi=5, ma=15),
...               vcmap=matplotlib.cm.gist_heat,
...               vorder=t, output="polblogs_trust_transitivity.pdf")
<...>

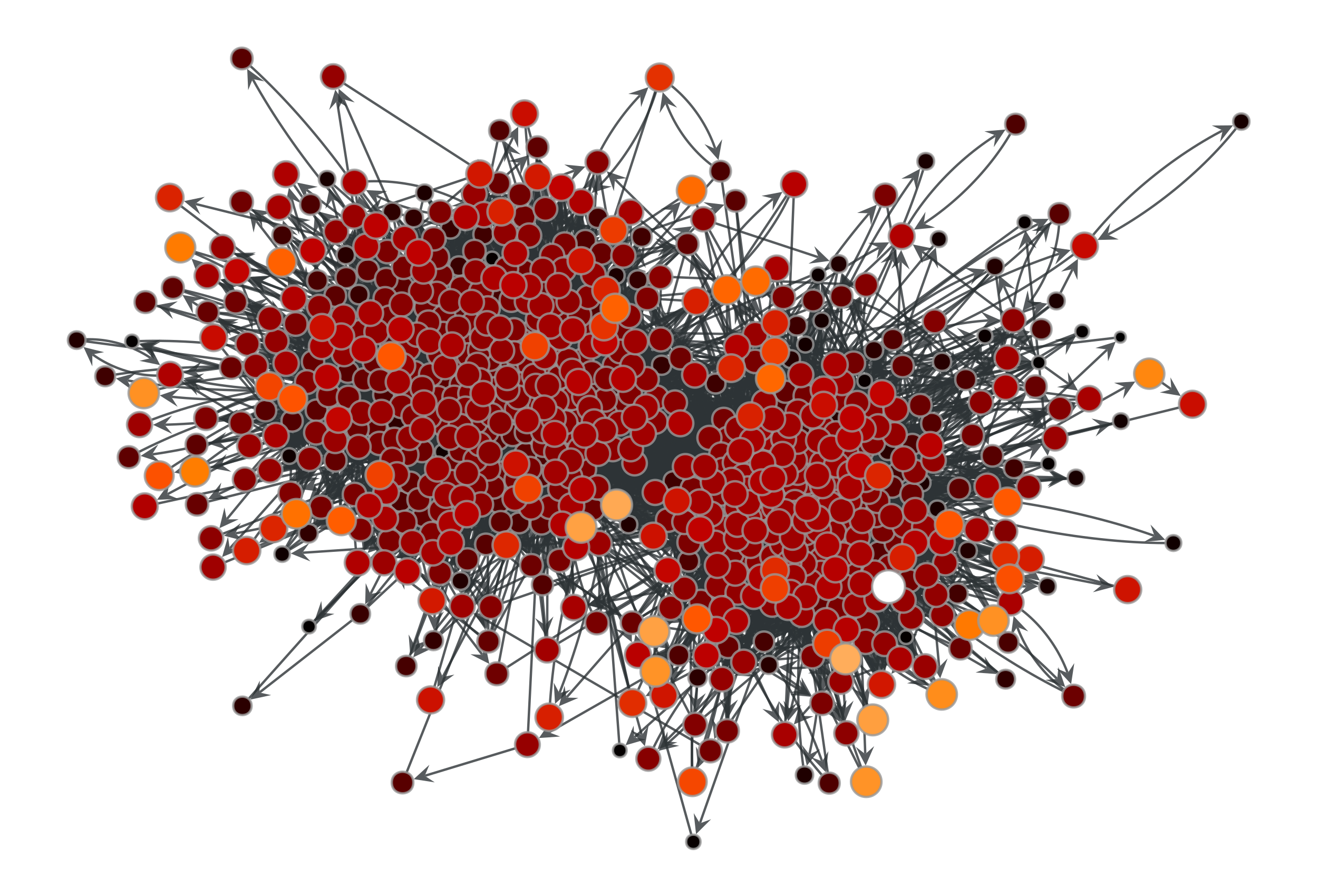
Trust transitivity values from source vertex 42 of the a political blogs network of [adamic-polblogs], with random weights attributed to the edges.