graph_merge#
- graph_tool.generation.graph_merge(g1, g2, eweight1=None, eweight2=None, vmap='identity', props={}, internal_props={}, in_place=False, multiset=False, diff=False, sym_diff=False, intersect=False, symmetric=False, fast_lookup=True, fast_symmetric=True, simple=False)[source]#
Merge the edges of graph
g2intog1, combining their weights, and including or excluding the edges according to the resulting weight.- Parameters:
- g1
Graph Graph to be merged into.
- g2
Graph Graph to be merged from.
- eweight1
EdgePropertyMap(optional, default:None) If provided, this will determine the weights of the edges of graph
g1. If not provided, each edge will be assumed to have unity weight.- eweight2
EdgePropertyMap(optional, default:None) If provided, this will determine the weights of the edges of graph
g2. If not provided, each edge will be assumed to have unity weight.- vmap
VertexPropertyMap,"identity", orNone(optional, default:None) Vertex property map owned by
g2which maps each of its vertices to vertex indices belonging tog1, in which case they are considered to be identical. Negative values mean no mapping exists, and thus both vertices ing1andg2will be present in the merged graph. If this argument is not provided (i.e.vmapisNone), both vertex sets will be added to the merge. Ifvmapisg2.vertex_index, and the vertex indexes are identical in both graphs, the merge will correspond only to the edge sets. A special value ofvmap == "identity"is a shortcut forvmap = g2.vertex_index.- propsdictionary with list of tuples of
PropertyMap(optional, default:{}) Property maps to be considered in the merge. The key in this dictionary must be a string indicating the merge rule:
"set"The value from
g2will be set, overwriting the value fromg1."sum"The value from
g2will be summed to the value fromg1."diff"The value from
g2will be subtracted from the value fromg1."idx_inc"The scalar value from
g2will be used as an index to increment the vector value fromg1by one. Alternatively, if the values fromg2are vectors, they will be interpreted as an(index, increment)pair. A negativeindexvalue means that the vector will be increased and its values shifted to the right by the absolute value ofindex, and the vector value at position0will be incremented."append"The scalar value from
g2will be appended to the vector value fromg1."concat"The vector value from
g2will be concatenated to the vector value fromg1.
The values of the dictionary must be lists, where each each element is a pair of
PropertyMapobjects. The first element must be a property ofg1, and the second ofg2. If either value isNone, an new map will be created, and set to appropriately empty values.The values of the property maps are propagated into the merged graph, and returned in a similar fashion.
- internal_propsdictionary with internal property names (optional, default:
{}) Internal property maps to be considered in the merge. The key in this dictionary must be a string indicating the merge rule, as documented in the
propsparameter.The values must be lists of
(k, name)pairs wherekis one of"e","v","g", for edge, vertex, or graph properties, respectively, and"name"is the name of the property map.An alternative value of
"all"indicates that all property maps should be considered. E.g.props = {"set": "all"}will set all the internal property maps to the merged graph.If an internal property map with the given name is not present in one of the graphs, an new map will be created, and set appropriately to empty values.
- in_place
bool(optional, default:False) If
True, graphg2is inserted in-place intog1, which is then modified. IfFalse, a new graph is created, and both graphs remain unmodified.- multiset
bool(optional, default:False) If
True, the edges in the merged graph will form a multiset, so that a single edge that exists in bothg1andg2becomes a parallel edge in the merged graph.- diff
bool(optional, default:False) If
Truethe weights of the merged edges will be the weights ofg1subtracted by those ofg2, otherwise they will be summed.- sym_diff
bool(optional, default:False) If
Truethe merged edges will have as weights the absolute difference between the weights of the edges ing1andg2.- intersect
bool(optional, default:False) If
Truean edge will be merged only if its weights in bothg1andg2are nonzero.- symmetric
bool(optional, default:False) If
Truethe edges ing1that are not present ing2will be removed, if they do not fulfill the merge conditions.- fast_lookup
bool(optional, default:True) If
Truefast edge lookup ing1will be enabled viaset_fast_edge_lookup().- fast_symmetric
bool(optional, default:True) If
Trueandsymmetric is True or simple is False, then fast edge lookup ing1will be enabled viaset_fast_edge_lookup().- simple
bool(optional, default:False) If
True, it will be assumed that bothg1andg2are simple graphs, for a faster version of the algorithm valid only in that case.
- g1
- Returns:
- ug
Graph The merged graph.
- w
EdgePropertyMap The edge weights of the merged graph. This is only returned if
eweight1is notNone.- propsdictionary with lists of
PropertyMapobjects List of properties in the merged graph, index by merge type. This is only returned if props is not empty. Internal property maps are not included in this list.
- ug
See also
graph_unionUnion of the edge sets between two graphs.
graph_differenceDifference of the edge sets between two graphs.
graph_sym_differenceSymmetrcic difference of the edge sets between two graphs.
graph_intersectionIntersection of the edge sets between two graphs.
condensation_graphObtain the condensation graph.
Notes
The algorithm runs in time \(O(N_1 + N_2 + E_1 + E_2)\), where \(N_1\), \(N_2\), \(E_1\), and \(E_2\) are the number of vertices and edges, for
g1andg2, respectively.If
symmetric is False,in_place is True, and eithermultiset is Trueor bothget_fast_edge_lookup()andget_fast_edge_removal()returnsTrueforg1, the algorithmic complexity becomes instead \(O(N_2 + E_2)\). In this situation it becomes efficient to merge a relatively small graphg2into an arbitrarily large graphg1.Parallel implementation.
If enabled during compilation, this algorithm will run in parallel using OpenMP. See the parallel algorithms section for information about how to control several aspects of parallelization.
Examples
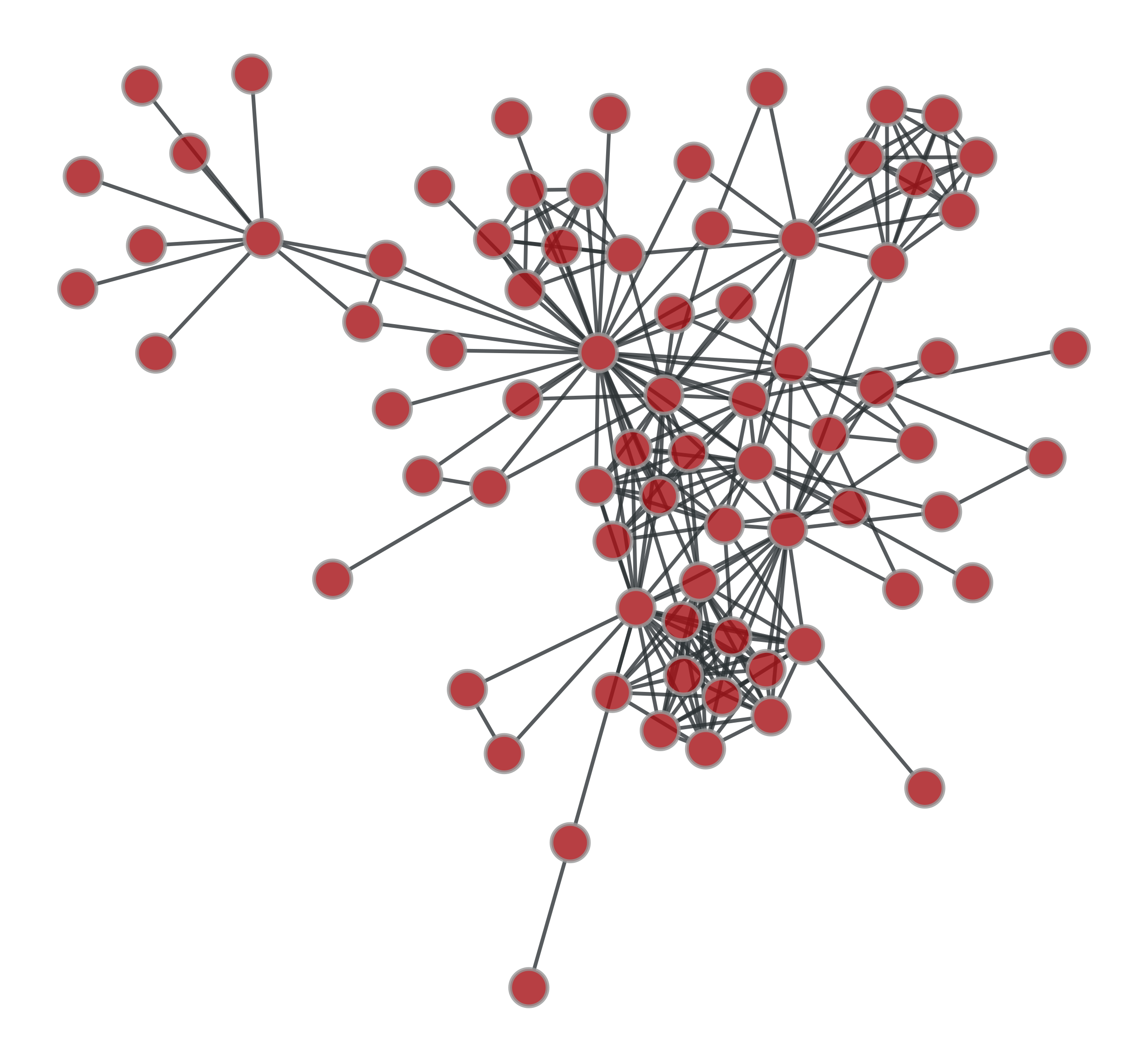
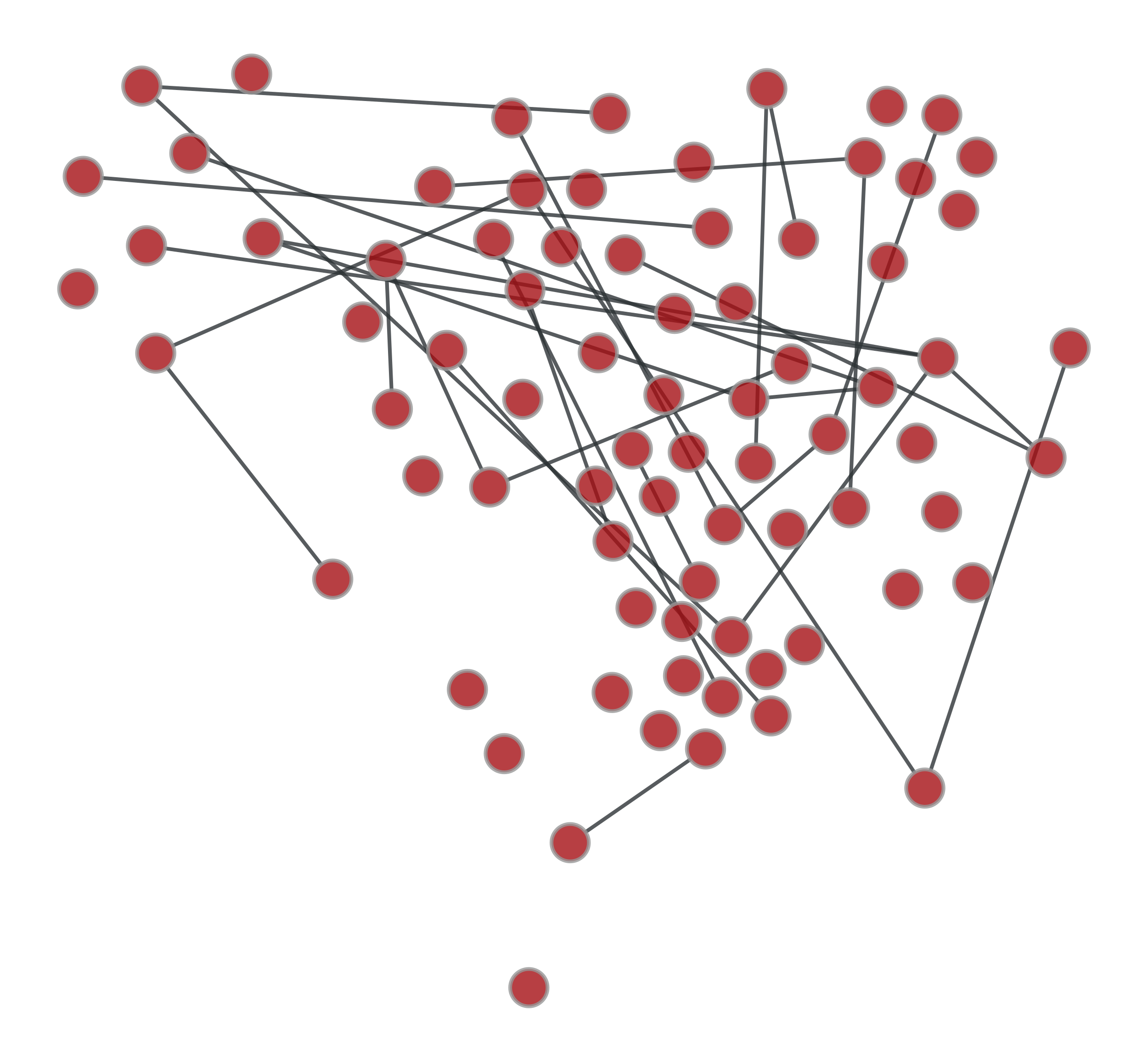
>>> g1 = gt.collection.ns["lesmis"] >>> g2 = gt.random_graph(77, lambda: np.random.poisson(1), directed=False, model="erdos") >>> label1 = g1.new_ep("int", val=0) >>> label2 = g2.new_ep("int", val=1) >>> u, ps = gt.graph_merge(g1, g2, props={"set": [(label1, label2)]}) >>> label = ps["set"][0] >>> gt.graph_draw(g1, pos=g1.vp._pos, output="g1.pdf") <...> >>> gt.graph_draw(g2, pos=g1.vp._pos, output="g2.pdf") <...> >>> gt.graph_draw(u, pos=u.own_property(g1.vp._pos), ... edge_color=label.t(lambda x: "black" if x == 0 else "blue", ... value_type="string", no_array=True), ... edge_pen_width=2, output="gmerge.pdf") <...>