max_cardinality_matching#
- graph_tool.topology.max_cardinality_matching(g, weight=None, bipartite=False, init_match='extra_greedy', heuristic=False, minimize=False, edges=False, brute_force=False)[source]#
Find a maximum cardinality matching in the graph.
- Parameters:
- g
Graph Graph to be used.
- weight
EdgePropertyMap(optional, default:None) If provided, the matching will maximize the sum of edge weights.
- bipartite
boolorVertexPropertyMap(optional, default:False) If
True, the graph will be assumed to be bipartite. If aVertexPropertyMapis passed, it should correspond to an existing bi-partition.- init_match
string(optional, default:"extra_greedy") Initial matching strategy. Can be one of: “empty”, “greedy”, “extra_greedy”. Ignored if
weightis given, orheuristic == True.- minimize
bool(optional, default:True) If
True, the matching will minimize the weights, otherwise they will be maximized. This option has no effect ifheuristic == False.- heuristic
bool(optional, default:False) If
True, a random heuristic will be used, which runs in linear time.- edges
bool(optional, default:False) If
True, an edge property map will be returned, instead of a vertex property map.- brute_force
bool(optional, default:False) If
True, andweightis notNoneandheuristicisFalse, a slower, brute-force algorithm is used.
- g
- Returns:
- match
VertexPropertyMap Vertex property map where the matching is specified. If
edges == Truea boolean-valued edge property map is returned instead.
- match
Notes
A matching is a subset of the edges of a graph such that no two edges share a common vertex. A maximum cardinality matching has maximum size over all matchings in the graph.
If the parameter
weightis provided, a matching with maximum cardinality and maximum weight is returned.If
heuristic == Truethe algorithm does not necessarily return the maximum matching, instead the focus is to run on linear time [matching-heuristic].This algorithm runs in time \(O(EV\times\alpha(E,V))\), where \(\alpha(m,n)\) is a slow growing function that is at most 4 for any feasible input.
If weights are given, the algorithm runs in time \(O(V^3)\).
If heuristic == True, the algorithm runs in time \(O(V + E)\).
If brute_force == True, the algorithm runs in time \(O(\exp(E))\).
For a more detailed description, see [boost-max-matching] and [boost-max-weighted-matching].
References
[matching-heuristic]B. Hendrickson and R. Leland. “A Multilevel Algorithm for Partitioning Graphs.” In S. Karin, editor, Proc. Supercomputing ’95, San Diego. ACM Press, New York, 1995, DOI: 10.1145/224170.224228 [sci-hub, @tor]
Examples
>>> g = gt.GraphView(gt.price_network(300), directed=False) >>> w = gt.max_cardinality_matching(g, edges=True) >>> gt.graph_draw(g, edge_color=w, edge_pen_width=w.t(lambda x: 2*x + 1), ... vertex_fill_color="grey", ecmap=matplotlib.cm.tab10, ... output="max_card_match.pdf") <...>
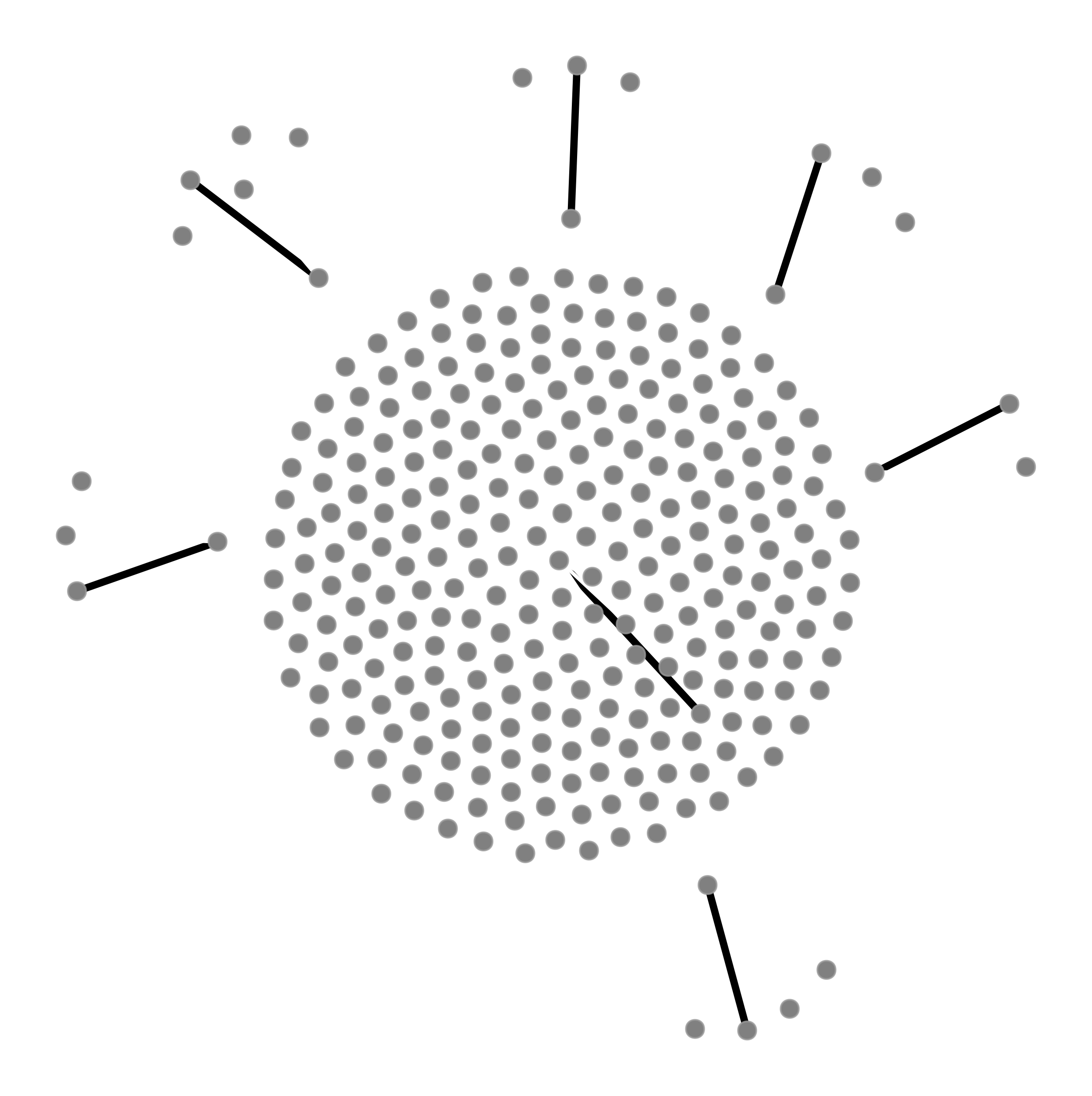
Edges belonging to the matching are drawn in orange.#