condensation_graph

graph_tool.generation.condensation_graph(g, prop, vweight=None, eweight=None, aprops=None, parallel_edges=False, **kwargs)

Obtain the condensation graph, where each vertex with the same ‘prop’ value is condensed in one vertex.

Parameters:

gGraph

Graph to be modelled.

propVertexPropertyMap

Vertex property map with the community partition (needs to be integer-valued).

vweightVertexPropertyMap (optional, default: None)

Vertex property map with the optional vertex weights.

eweightEdgePropertyMap (optional, default: None)

Edge property map with the optional edge weights.

apropslist of VertexPropertyMap (optional, default: None)

If provided, the sum of each property map in this list for each vertex or edge in the condensed graph will be computed and returned.

parallel_edgesbool (optional, default: False)

If True, parallel edges will be included in the condensation graph, such that the total number of edges will be the same as in the original graph.

Returns:

condensation_graphGraph

The community network

vcountVertexPropertyMap

A vertex property map with the vertex count for each community.

ecountEdgePropertyMap

An edge property map with the inter-community edge count for each edge.

propslist of PropertyMap

A list of property maps with summed values of the properties passed via the aprops parameter.

See also

graph_merge

Merge the edge sets between two graphs.

Notes

Each vertex in the condensation graph represents one community in the original graph (vertices with the same ‘prop’ value), and the edges represent existent edges between vertices of the respective communities in the original graph.

This algorithm is a wrapper around graph_merge(), and shares with it the same algorithmic complexity.

Parallel implementation.

If enabled during compilation, this algorithm will run in parallel using OpenMP. See the parallel algorithms section for information about how to control several aspects of parallelization.

Examples

Let’s first obtain the best block partition with B=5.

>>> g = gt.collection.data["polbooks"]
>>> # fit a SBM
>>> state = gt.BlockState(g)
>>> gt.mcmc_equilibrate(state, wait=1000)
(...)
>>> b = state.get_blocks()
>>> b = gt.perfect_prop_hash([b])[0]
>>> gt.graph_draw(g, pos=g.vp["pos"], vertex_fill_color=b, vertex_shape=b,
...               output="polbooks_blocks_B5.pdf")
<...>

Now we get the condensation graph:

>>> bg, vcount, ecount, props = \
...     gt.condensation_graph(g, b, aprops=[g.vp["pos"]])
>>> pos = props[0]
>>> for v in bg.vertices():
...     pos[v].a /= vcount[v]
>>> gt.graph_draw(bg, pos=pos, vertex_fill_color=bg.vertex_index,
...               vertex_shape=bg.vertex_index,
...               vertex_size=gt.prop_to_size(vcount, mi=40, ma=100),
...               edge_pen_width=gt.prop_to_size(ecount, mi=2, ma=10),
...               fit_view=.8, output="polbooks_blocks_B5_cond.pdf")
<...>

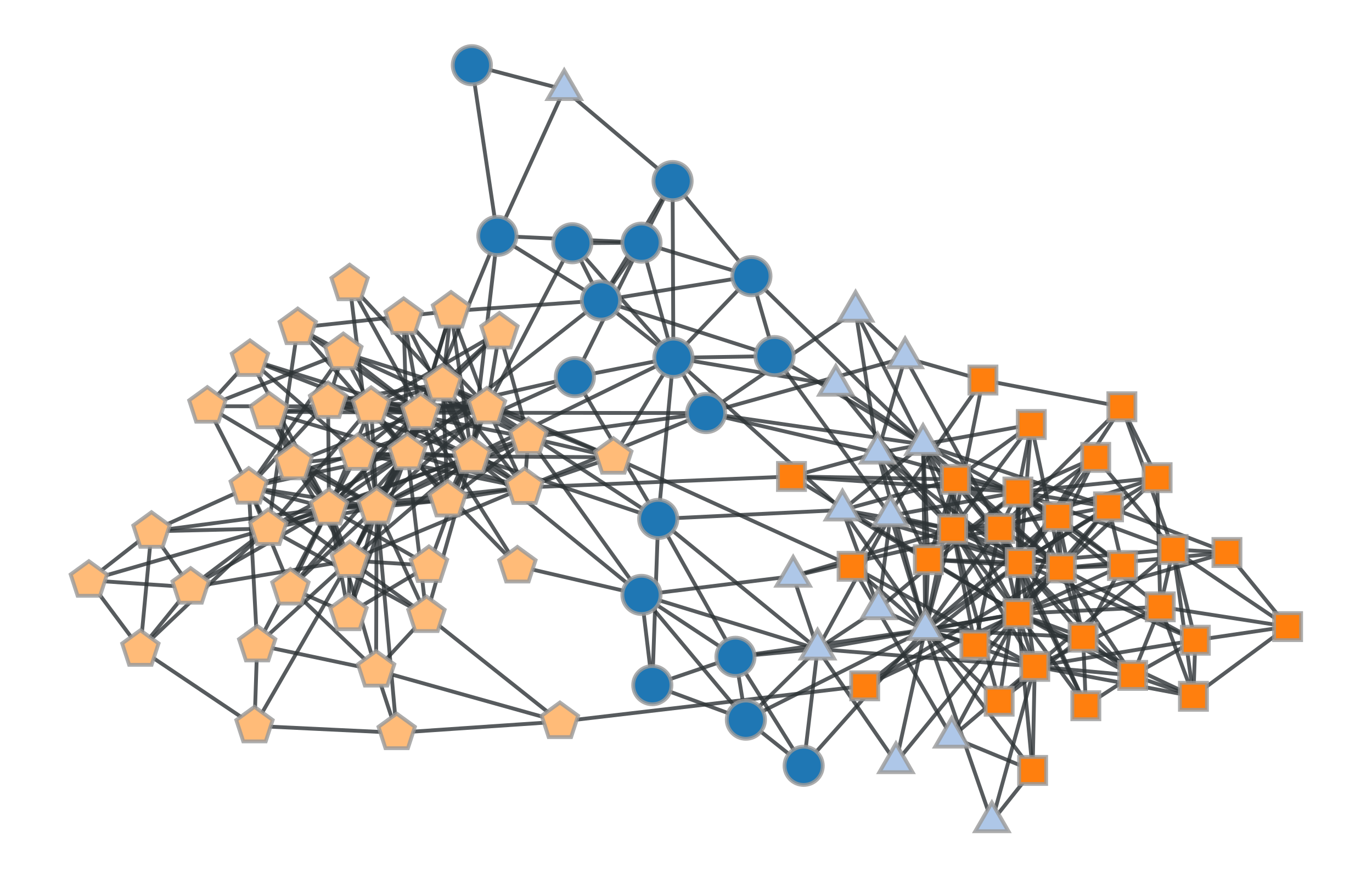
Block partition of a political books network with \(B=5\).

Condensation graph of the obtained block partition.