minimize_blockmodel_dl

graph_tool.inference.minimize_blockmodel_dl(g, state=<class 'graph_tool.inference.blockmodel.BlockState'>, state_args={}, multilevel_mcmc_args={})

Fit the stochastic block model, by minimizing its description length using an agglomerative heuristic.

Parameters:

gGraph

The graph.

stateSBM-like state class (optional, default: BlockState)

Type of model that will be used. Must be derived from MultilevelMCMCState.

state_argsdict (optional, default: {})

Arguments to be passed to appropriate state constructor (e.g. BlockState)

multilevel_mcmc_argsdict (optional, default: {})

Arguments to be passed to multilevel_mcmc_sweep().

Returns:

min_statetype given by parameter state

State with minimum description length.

Notes

This function is a convenience wrapper around multilevel_mcmc_sweep().

See [peixoto-efficient-2014] for details on the algorithm.

This algorithm has a complexity of \(O(V \ln^2 V)\), where \(V\) is the number of nodes in the network.

References

[peixoto-efficient-2014]

Tiago P. Peixoto, “Efficient Monte Carlo and greedy heuristic for the inference of stochastic block models”, Phys. Rev. E 89, 012804 (2014), DOI: 10.1103/PhysRevE.89.012804 [sci-hub, @tor], arXiv: 1310.4378.

Examples

>>> g = gt.collection.data["polbooks"]
>>> state = gt.minimize_blockmodel_dl(g)
>>> state.draw(pos=g.vp["pos"], vertex_shape=state.get_blocks(),
...            output="polbooks_blocks_mdl.svg")
<...>

Block partition of a political books network, which minimizes the description length of the network according to the degree-corrected stochastic blockmodel.

>>> g = gt.collection.data["polbooks"]
>>> state = gt.minimize_blockmodel_dl(g, state=gt.OverlapBlockState)
>>> state.draw(pos=g.vp["pos"], output="polbooks_overlap_blocks_mdl.svg")
<...>

Overlapping partition of a political books network, which minimizes the description length of the network according to the overlapping degree-corrected stochastic blockmodel.

>>> g = gt.collection.data["celegansneural"]
>>> state = gt.minimize_blockmodel_dl(g, state=gt.PPBlockState)
>>> state.draw(output="celegans_mdl_pp.pdf")
<...>

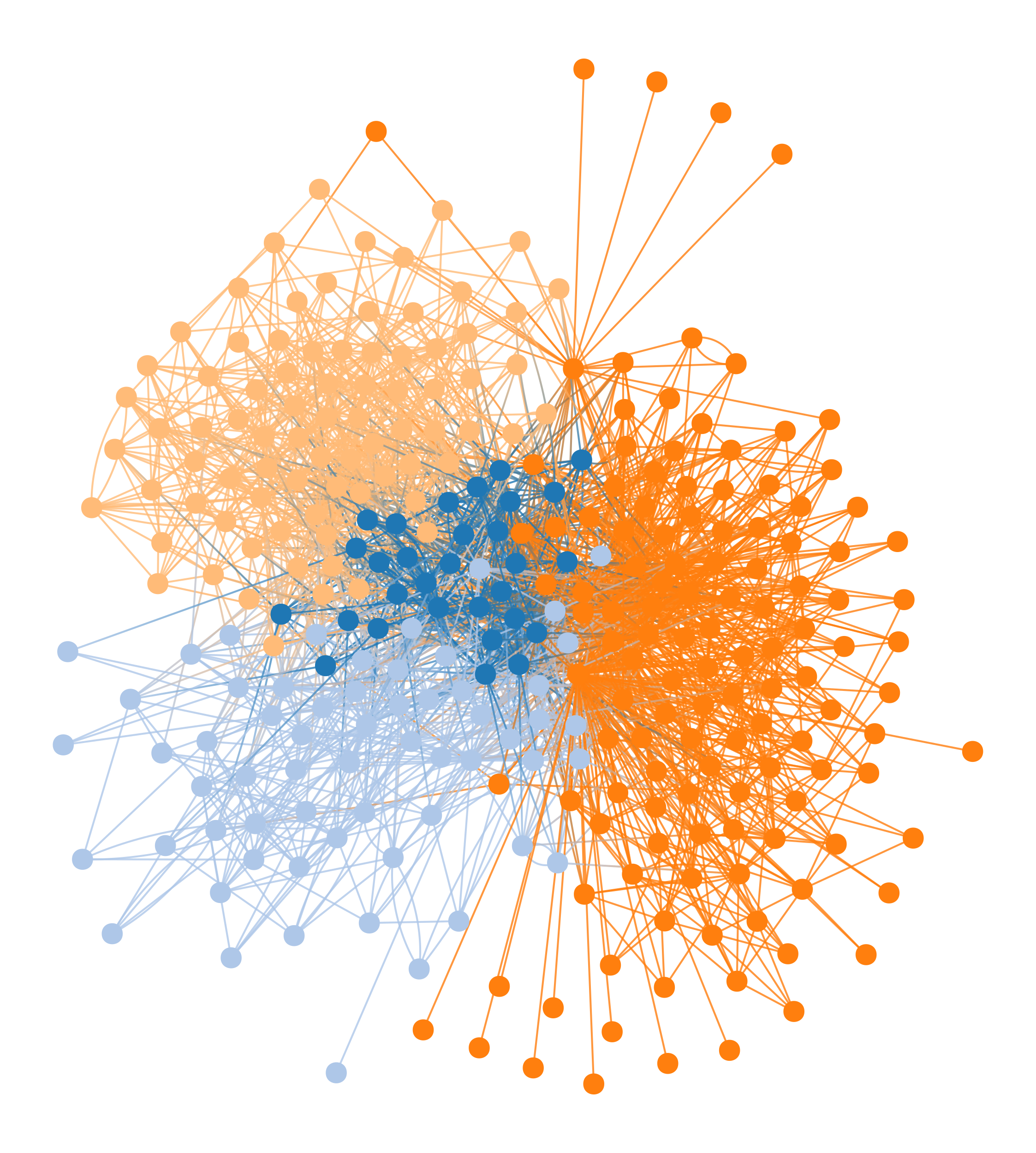
Assortative partition of the C. elegans neural network, which minimizes the description length of the network according to the degree-corrected planted-partition blockmodel.