edmonds_karp_max_flow

edmonds_karp_max_flow#

graph_tool.flow.edmonds_karp_max_flow(g, source, target, capacity, residual=None)[source]#

Calculate maximum flow on the graph with the Edmonds-Karp algorithm.

Parameters:
gGraph

Graph to be used.

sourceVertex

The source vertex.

targetVertex

The target (or “sink”) vertex.

capacityEdgePropertyMap

Edge property map with the edge capacities.

residualEdgePropertyMap (optional, default: none)

Edge property map where the residuals should be stored.

Returns:
residualEdgePropertyMap

Edge property map with the residual capacities (capacity - flow).

Notes

The algorithm is due to [edmonds-theoretical-1972], though we are using the variation called the “labeling algorithm” described in [ravindra-network-1993].

This algorithm provides a very simple and easy to implement solution to the maximum flow problem. However, there are several reasons why this algorithm is not as good as the push_relabel_max_flow() or the boykov_kolmogorov_max_flow() algorithm.

  • In the non-integer capacity case, the time complexity is \(O(VE^2)\) which is worse than the time complexity of the push-relabel algorithm \(O(V^2E^{1/2})\) for all but the sparsest of graphs.

  • In the integer capacity case, if the capacity bound U is very large then the algorithm will take a long time.

The time complexity is \(O(VE^2)\) in the general case or \(O(VEU)\) if capacity values are integers bounded by some constant \(U\).

References

[edmonds-theoretical-1972]

Jack Edmonds and Richard M. Karp, “Theoretical improvements in the algorithmic efficiency for network flow problems. Journal of the ACM”, 19:248-264, 1972 DOI: 10.1145/321694.321699 [sci-hub, @tor]

[ravindra-network-1993]

Ravindra K. Ahuja and Thomas L. Magnanti and James B. Orlin,”Network Flows: Theory, Algorithms, and Applications”. Prentice Hall, 1993.

Examples

>>> g = gt.load_graph("flow-example.xml.gz")
>>> cap = g.edge_properties["cap"]
>>> src, tgt = g.vertex(0), g.vertex(1)
>>> res = gt.edmonds_karp_max_flow(g, src, tgt, cap)
>>> res.a = cap.a - res.a  # the actual flow
>>> max_flow = sum(res[e] for e in tgt.in_edges())
>>> print(max_flow)
44.8905957841...
>>> pos = g.vertex_properties["pos"]
>>> gt.graph_draw(g, pos=pos, edge_pen_width=gt.prop_to_size(res, mi=0, ma=5, power=1), output="example-edmonds-karp.pdf")
<...>
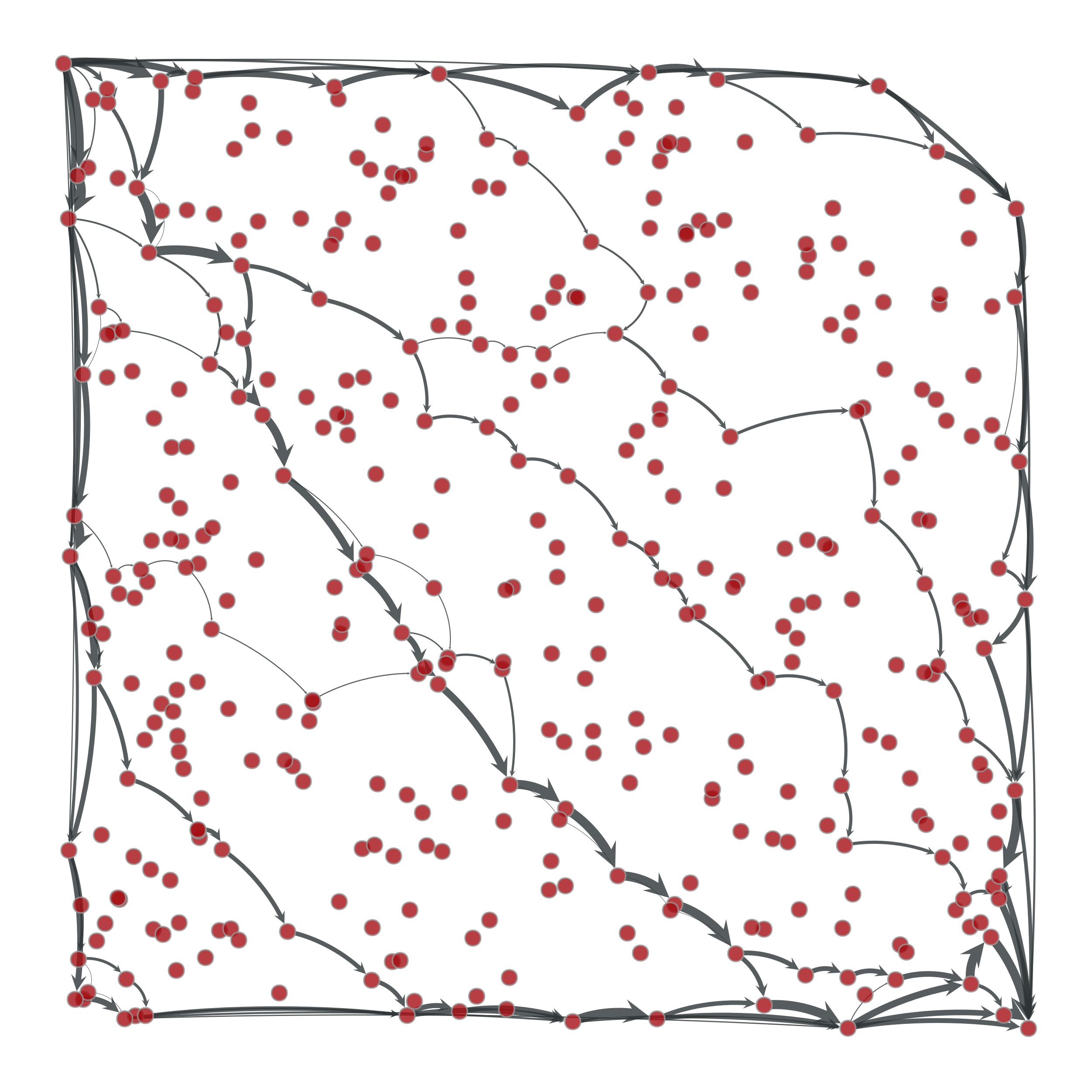
../_images/example-edmonds-karp.png

Edge flows obtained with the Edmonds-Karp algorithm. The source and target are on the upper left and lower right corners, respectively. The edge flows are represented by the edge width.#