min_spanning_tree

min_spanning_tree#

graph_tool.topology.min_spanning_tree(g, weights=None, root=None, tree_map=None)[source]#

Return the minimum spanning tree of a given graph.

Parameters:
gGraph

Graph to be used.

weightsEdgePropertyMap (optional, default: None)

The edge weights. If provided, the minimum spanning tree will minimize the edge weights.

rootVertex (optional, default: None)

Root of the minimum spanning tree. If this is provided, Prim’s algorithm is used. Otherwise, Kruskal’s algorithm is used.

tree_mapEdgePropertyMap (optional, default: None)

If provided, the edge tree map will be written in this property map.

Returns:
tree_mapEdgePropertyMap

Edge property map with mark the tree edges: 1 for tree edge, 0 otherwise.

Notes

The algorithm runs with \(O(E\log E)\) complexity, or \(O(E\log V)\) if root is specified.

References

[kruskal-shortest-1956]

J. B. Kruskal. “On the shortest spanning subtree of a graph and the traveling salesman problem”, In Proceedings of the American Mathematical Society, volume 7, pages 48-50, 1956. DOI: 10.1090/S0002-9939-1956-0078686-7 [sci-hub, @tor]

[prim-shortest-1957]

R. Prim. “Shortest connection networks and some generalizations”, Bell System Technical Journal, 36:1389-1401, 1957.

Examples

>>> from numpy.random import random
>>> g, pos = gt.triangulation(random((400, 2)) * 10, type="delaunay")
>>> weight = g.new_edge_property("double")
>>> for e in g.edges():
...    weight[e] = linalg.norm(pos[e.target()].a - pos[e.source()].a)
>>> tree = gt.min_spanning_tree(g, weights=weight)
>>> gt.graph_draw(g, pos=pos, output="triang_orig.pdf")
<...>
>>> u = gt.GraphView(g, efilt=tree)
>>> gt.graph_draw(u, pos=pos, output="triang_min_span_tree.pdf")
<...>
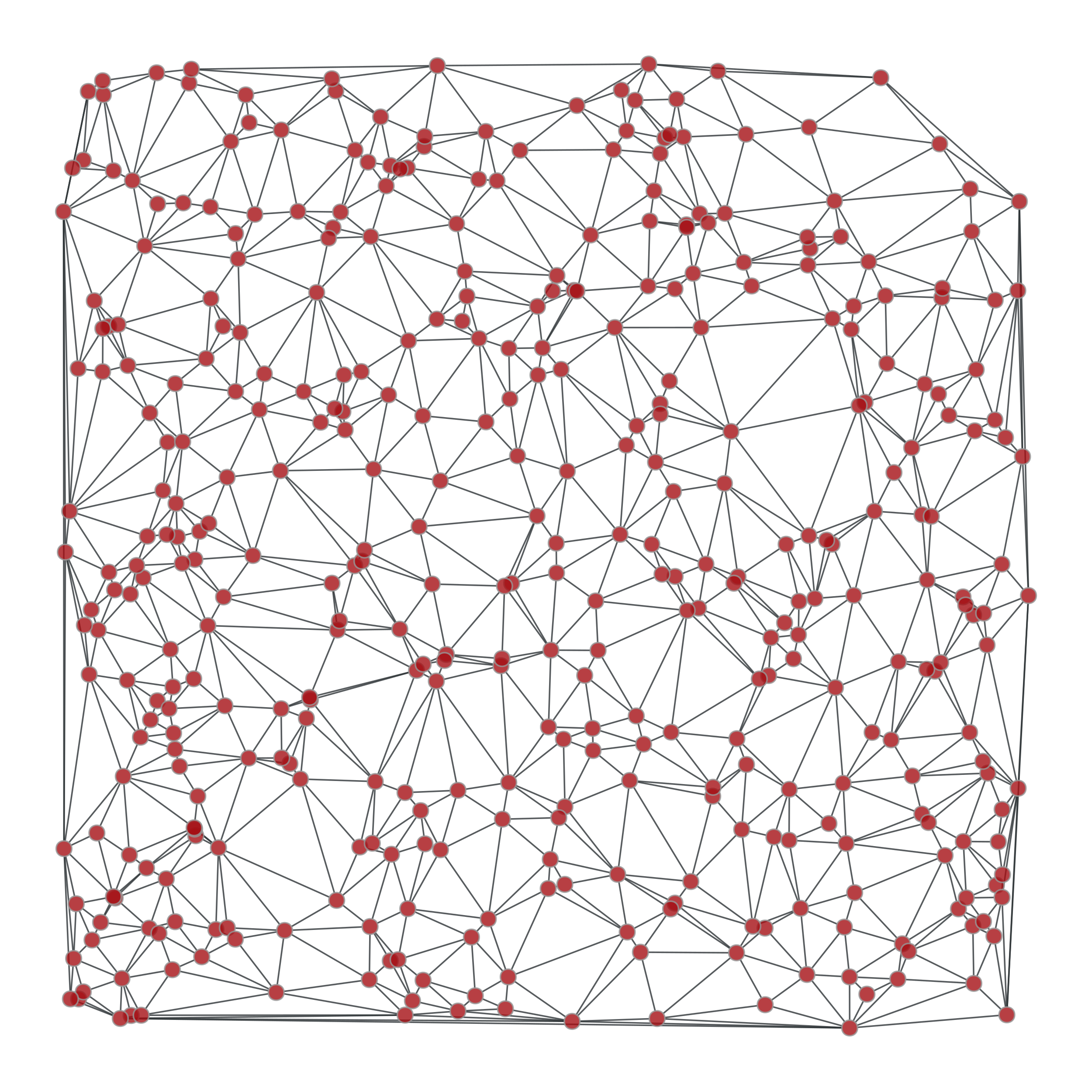
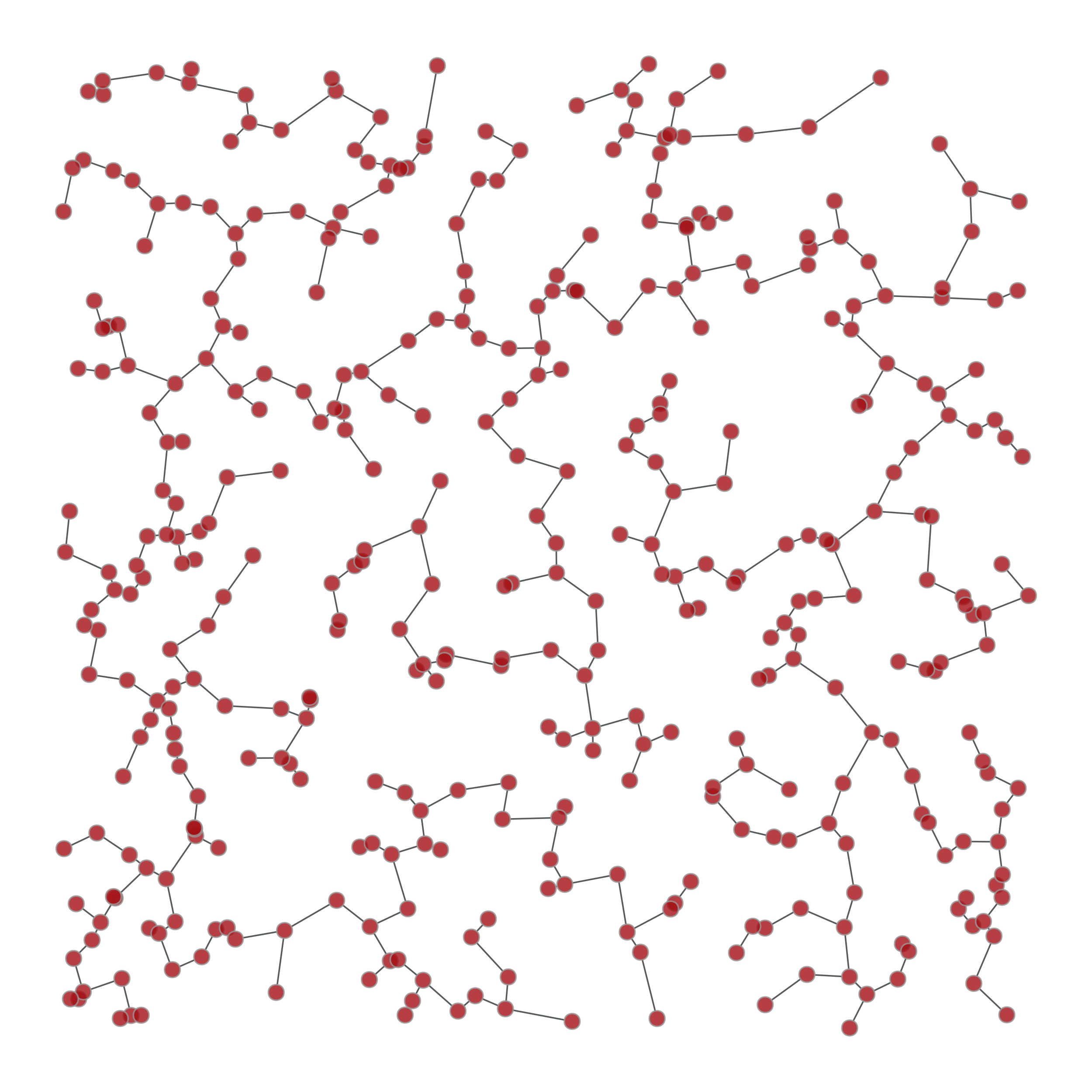
../_images/triang_orig.png ../_images/triang_min_span_tree.png

Left: Original graph, Right: The minimum spanning tree.