pagerank#
- graph_tool.centrality.pagerank(g, damping=0.85, pers=None, weight=None, prop=None, epsilon=1e-06, max_iter=None, ret_iter=False)[source]#
Calculate the PageRank of each vertex.
- Parameters:
- g
Graph Graph to be used.
- dampingfloat, optional (default: 0.85)
Damping factor.
- pers
VertexPropertyMap, optional (default: None) Personalization vector. If omitted, a constant value of \(1/N\) will be used.
- weight
EdgePropertyMap, optional (default: None) Edge weights. If omitted, a constant value of 1 will be used.
- prop
VertexPropertyMap, optional (default: None) Vertex property map to store the PageRank values. If supplied, it will be used uninitialized.
- epsilonfloat, optional (default: 1e-6)
Convergence condition. The iteration will stop if the total delta of all vertices are below this value.
- max_iterint, optional (default: None)
If supplied, this will limit the total number of iterations.
- ret_iterbool, optional (default: False)
If true, the total number of iterations is also returned.
- g
- Returns:
- pagerank
VertexPropertyMap A vertex property map containing the PageRank values.
- pagerank
See also
betweennessbetweenness centrality
eigentrusteigentrust centrality
eigenvectoreigenvector centrality
hitsauthority and hub centralities
trust_transitivitypervasive trust transitivity
Notes
The value of PageRank [pagerank-wikipedia] of vertex v, \(PR(v)\), is given iteratively by the relation:
\[PR(v) = \frac{1-d}{N} + d \sum_{u \in \Gamma^{-}(v)} \frac{PR (u)}{d^{+}(u)}\]where \(\Gamma^{-}(v)\) are the in-neighbors of v, \(d^{+}(u)\) is the out-degree of u, and d is a damping factor.
If a personalization property \(p(v)\) is given, the definition becomes:
\[PR(v) = (1-d)p(v) + d \sum_{u \in \Gamma^{-}(v)} \frac{PR (u)}{d^{+}(u)}\]If edge weights are also given, the equation is then generalized to:
\[PR(v) = (1-d)p(v) + d \sum_{u \in \Gamma^{-}(v)} \frac{PR (u) w_{u\to v}}{d^{+}(u)}\]where \(d^{+}(u)=\sum_{y}A_{u,y}w_{u\to y}\) is redefined to be the sum of the weights of the out-going edges from u.
If a node has out-degree zero, it is assumed to connect to every other node with a weight proportional to \(p(v)\) or a constant if no personalization is given.
The implemented algorithm progressively iterates the above equations, until it no longer changes, according to the parameter epsilon. It has a topology-dependent running time.
Parallel implementation.
If enabled during compilation, this algorithm will run in parallel using OpenMP. See the parallel algorithms section for information about how to control several aspects of parallelization.
References
[lawrence-pagerank-1998]P. Lawrence, B. Sergey, M. Rajeev, W. Terry, “The pagerank citation ranking: Bringing order to the web”, Technical report, Stanford University, 1998
[Langville-survey-2005]A. N. Langville, C. D. Meyer, “A Survey of Eigenvector Methods for Web Information Retrieval”, SIAM Review, vol. 47, no. 1, pp. 135-161, 2005, DOI: 10.1137/S0036144503424786 [sci-hub, @tor]
[adamic-polblogs] (1,2)L. A. Adamic and N. Glance, “The political blogosphere and the 2004 US Election”, in Proceedings of the WWW-2005 Workshop on the Weblogging Ecosystem (2005). DOI: 10.1145/1134271.1134277 [sci-hub, @tor]
Examples
>>> g = gt.collection.data["polblogs"] >>> g = gt.GraphView(g, vfilt=gt.label_largest_component(g)) >>> pr = gt.pagerank(g) >>> gt.graph_draw(g, pos=g.vp["pos"], vertex_fill_color=pr, ... vertex_size=gt.prop_to_size(pr, mi=5, ma=15), ... vorder=pr, vcmap=matplotlib.cm.gist_heat, ... output="polblogs_pr.pdf") <...>
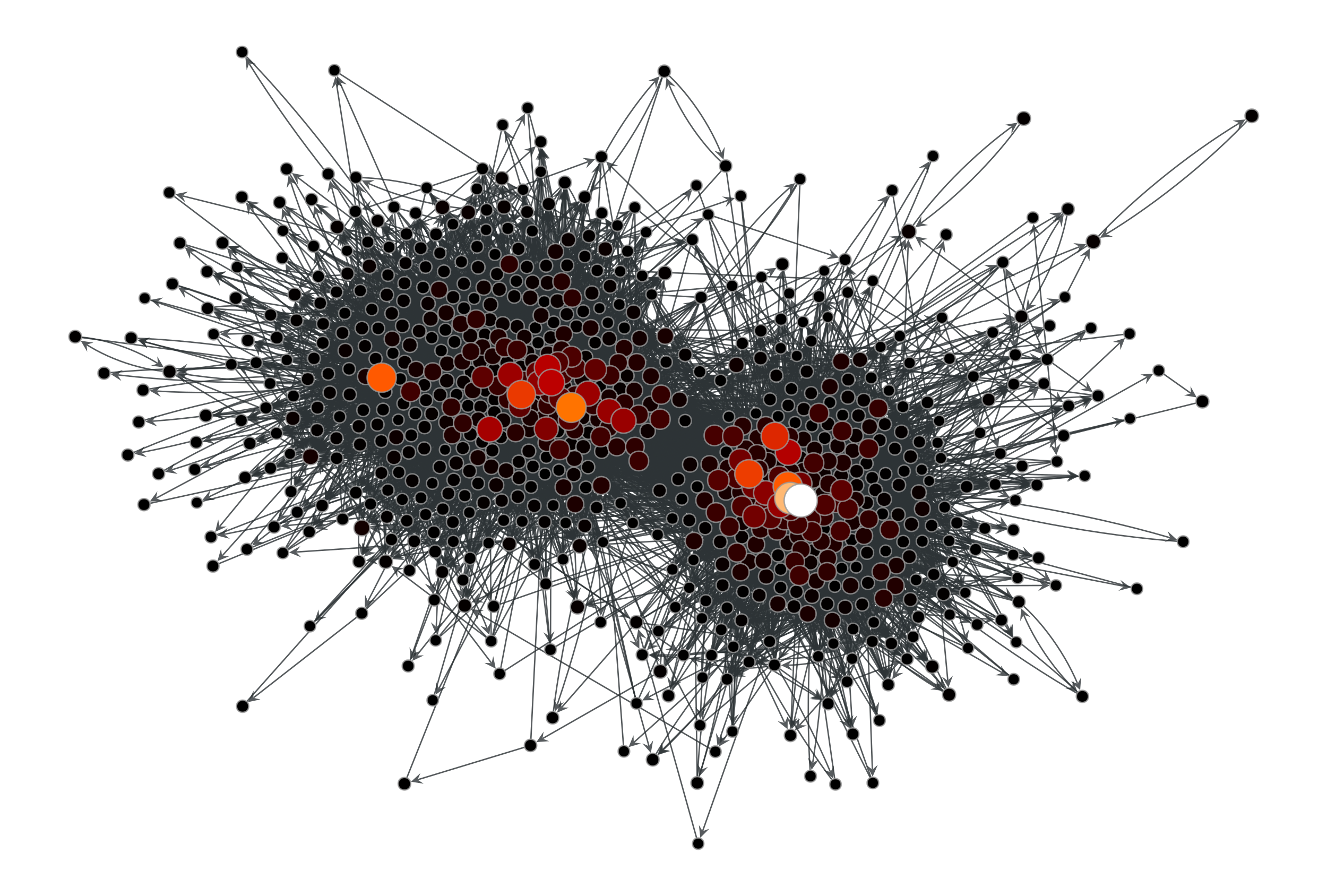
PageRank values of the a political blogs network of [adamic-polblogs].#
Now with a personalization vector, and edge weights:
>>> d = g.degree_property_map("total") >>> periphery = d.a <= 2 >>> p = g.new_vertex_property("double") >>> p.a[periphery] = 100 >>> pr = gt.pagerank(g, pers=p) >>> gt.graph_draw(g, pos=g.vp["pos"], vertex_fill_color=pr, ... vertex_size=gt.prop_to_size(pr, mi=5, ma=15), ... vorder=pr, vcmap=matplotlib.cm.gist_heat, ... output="polblogs_pr_pers.pdf") <...>

Personalized PageRank values of the a political blogs network of [adamic-polblogs], where vertices with very low degree are given artificially high scores.#