graph_tool.centrality.hits

graph_tool.centrality.hits(g, weight=None, xprop=None, yprop=None, epsilon=1e-06, max_iter=None)

Calculate the authority and hub centralities of each vertex in the graph.

Parameters:

gGraph

Graph to be used.

weightEdgePropertyMap (optional, default: None)

Edge property map with the edge weights.

xpropVertexPropertyMap, optional (default: None)

Vertex property map where the authority centrality must be stored.

ypropVertexPropertyMap, optional (default: None)

Vertex property map where the hub centrality must be stored.

epsilonfloat, optional (default: 1e-6)

Convergence condition. The iteration will stop if the total delta of all vertices are below this value.

max_iterint, optional (default: None)

If supplied, this will limit the total number of iterations.

Returns:

eigfloat

The largest eigenvalue of the cocitation matrix.

xVertexPropertyMap

A vertex property map containing the authority centrality values.

yVertexPropertyMap

A vertex property map containing the hub centrality values.

See also

betweenness

betweenness centrality

eigenvector

eigenvector centrality

pagerank

PageRank centrality

trust_transitivity

pervasive trust transitivity

Notes

The Hyperlink-Induced Topic Search (HITS) centrality assigns hub (\(\mathbf{y}\)) and authority (\(\mathbf{x}\)) centralities to the vertices, following:

\[\begin{split}\begin{align} \mathbf{x} &= \alpha\mathbf{A}\mathbf{y} \\ \mathbf{y} &= \beta\mathbf{A}^T\mathbf{x} \end{align}\end{split}\]

where \(\mathbf{A}\) is the (weighted) adjacency matrix and \(\lambda = 1/(\alpha\beta)\) is the largest eigenvalue of the cocitation matrix, \(\mathbf{A}\mathbf{A}^T\). (Without loss of generality, we set \(\beta=1\) in the algorithm.)

The algorithm uses the power method which has a topology-dependent complexity of \(O\left(N\times\frac{-\log\epsilon}{\log|\lambda_1/\lambda_2|}\right)\), where \(N\) is the number of vertices, \(\epsilon\) is the epsilon parameter, and \(\lambda_1\) and \(\lambda_2\) are the largest and second largest eigenvalues of the (weighted) cocitation matrix, respectively.

If enabled during compilation, this algorithm runs in parallel.

References

[hits-algorithm]

http://en.wikipedia.org/wiki/HITS_algorithm

[kleinberg-authoritative]

J. Kleinberg, “Authoritative sources in a hyperlinked environment”, Journal of the ACM 46 (5): 604-632, 1999, DOI: 10.1145/324133.324140 [sci-hub, @tor].

[power-method]

http://en.wikipedia.org/wiki/Power_iteration

[adamic-polblogs] (1,2)

L. A. Adamic and N. Glance, “The political blogosphere and the 2004 US Election”, in Proceedings of the WWW-2005 Workshop on the Weblogging Ecosystem (2005). DOI: 10.1145/1134271.1134277 [sci-hub, @tor]

Examples

>>> g = gt.collection.data["polblogs"]
>>> g = gt.GraphView(g, vfilt=gt.label_largest_component(g))
>>> ee, x, y = gt.hits(g)
>>> gt.graph_draw(g, pos=g.vp["pos"], vertex_fill_color=x,
...               vertex_size=gt.prop_to_size(x, mi=5, ma=15),
...               vcmap=matplotlib.cm.gist_heat,
...               vorder=x, output="polblogs_hits_auths.pdf")
<...>
>>> gt.graph_draw(g, pos=g.vp["pos"], vertex_fill_color=y,
...               vertex_size=gt.prop_to_size(y, mi=5, ma=15),
...               vcmap=matplotlib.cm.gist_heat,
...               vorder=y, output="polblogs_hits_hubs.pdf")
<...>

HITS authority values of the a political blogs network of [adamic-polblogs].

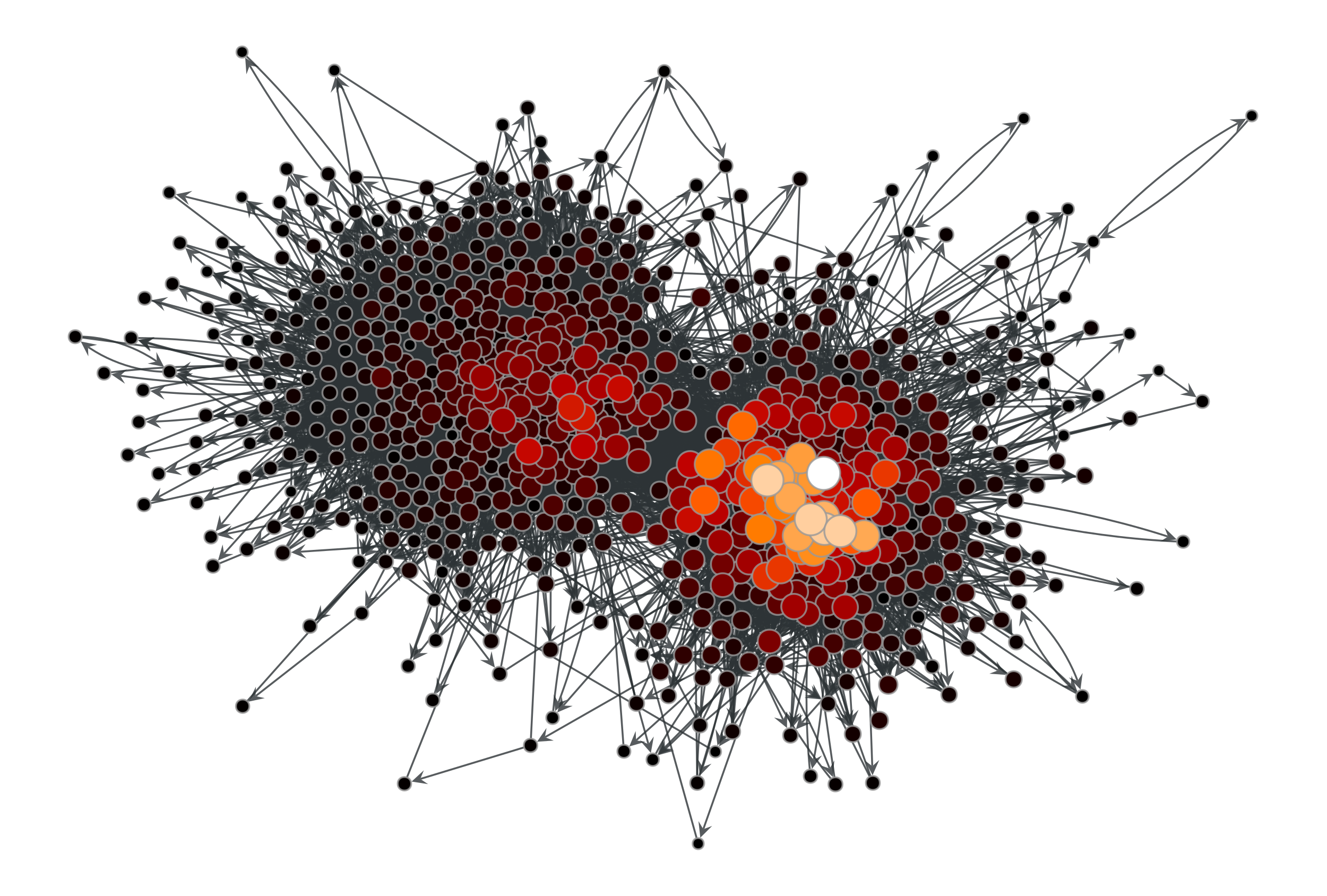
HITS hub values of the a political blogs network of [adamic-polblogs].