random_spanning_tree

random_spanning_tree#

graph_tool.topology.random_spanning_tree(g, weights=None, root=None, tree_map=None)[source]#

Return a random spanning tree of a given graph, which can be directed or undirected.

Parameters:
gGraph

Graph to be used.

weightsEdgePropertyMap (optional, default: None)

The edge weights. If provided, the probability of a particular spanning tree being selected is the product of its edge weights.

rootVertex (optional, default: None)

Root of the spanning tree. If not provided, it will be selected randomly.

tree_mapEdgePropertyMap (optional, default: None)

If provided, the edge tree map will be written in this property map.

Returns:
tree_mapEdgePropertyMap

Edge property map with mark the tree edges: 1 for tree edge, 0 otherwise.

Notes

The running time for this algorithm is \(O(\tau)\), with \(\tau\) being the mean hitting time of a random walk on the graph. In the worst case, we have \(\tau \sim O(V^3)\), with \(V\) being the number of vertices in the graph. However, in much more typical cases (e.g. sparse random graphs) the running time is simply \(O(V)\).

References

[wilson-generating-1996]

David Bruce Wilson, “Generating random spanning trees more quickly than the cover time”, Proceedings of the twenty-eighth annual ACM symposium on Theory of computing, Pages 296-303, ACM New York, 1996, DOI: 10.1145/237814.237880 [sci-hub, @tor]

Examples

>>> from numpy.random import random
>>> g, pos = gt.triangulation(random((400, 2)), type="delaunay")
>>> weight = g.new_edge_property("double")
>>> for e in g.edges():
...    weight[e] = linalg.norm(pos[e.target()].a - pos[e.source()].a)
>>> tree = gt.random_spanning_tree(g, weights=weight)
>>> tree2 = gt.random_spanning_tree(g, weights=weight)
>>> gt.graph_draw(g, pos=pos, output="rtriang_orig.pdf")
<...>
>>> u = gt.GraphView(g, efilt=tree)
>>> gt.graph_draw(u, pos=pos, output="triang_random_span_tree.pdf")
<...>
>>> u2 = gt.GraphView(g, efilt=tree2)
>>> gt.graph_draw(u2, pos=pos, output="triang_random_span_tree2.pdf")
<...>
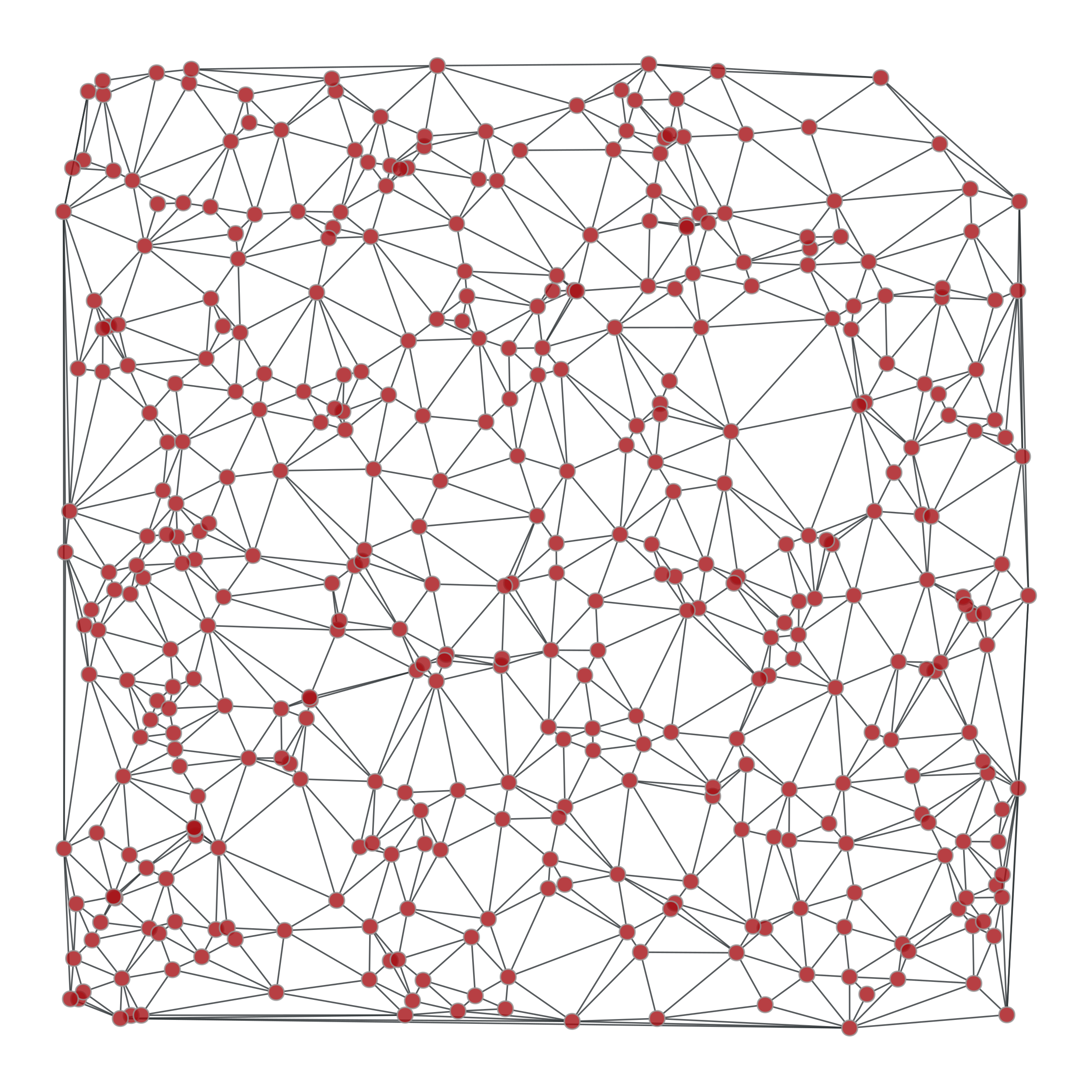
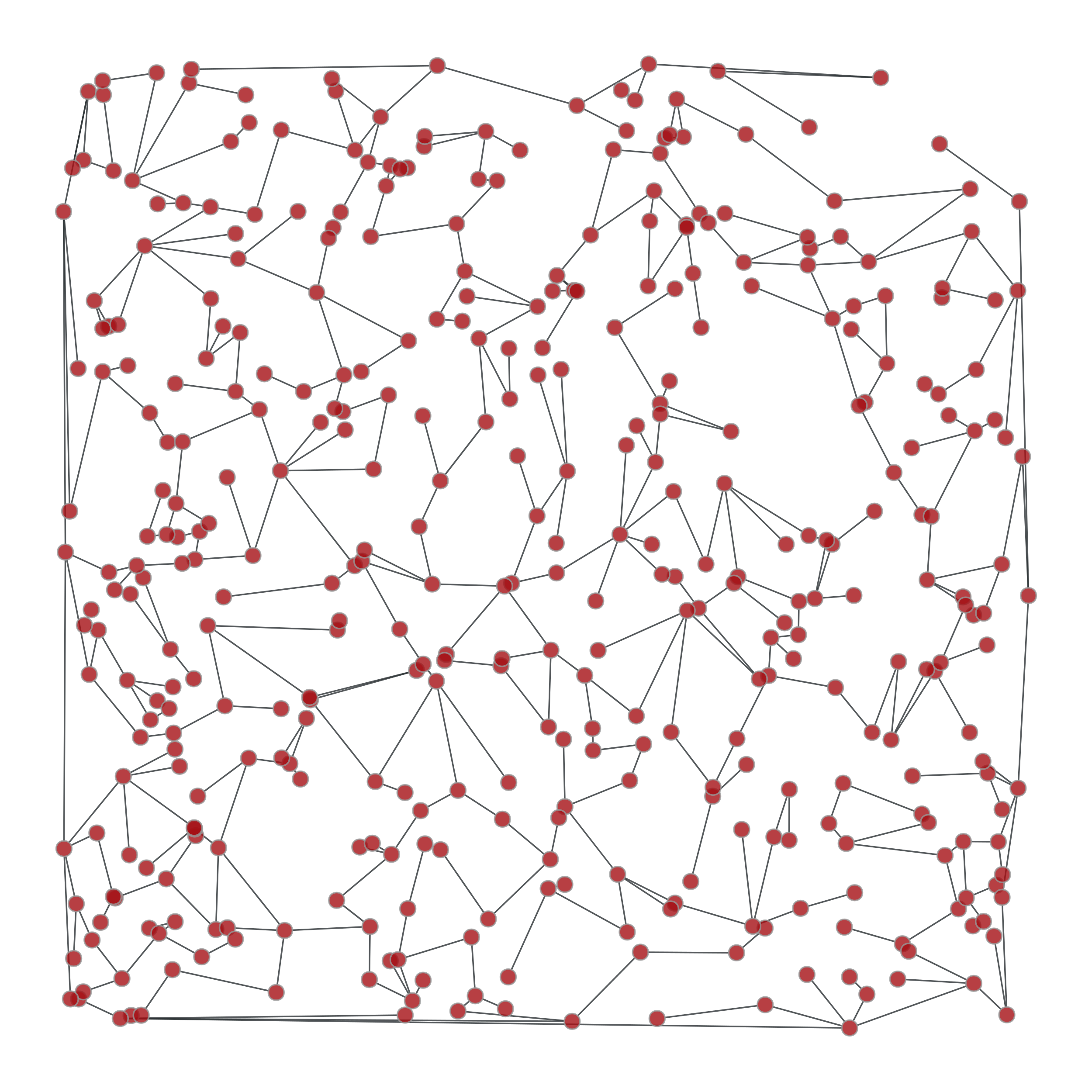
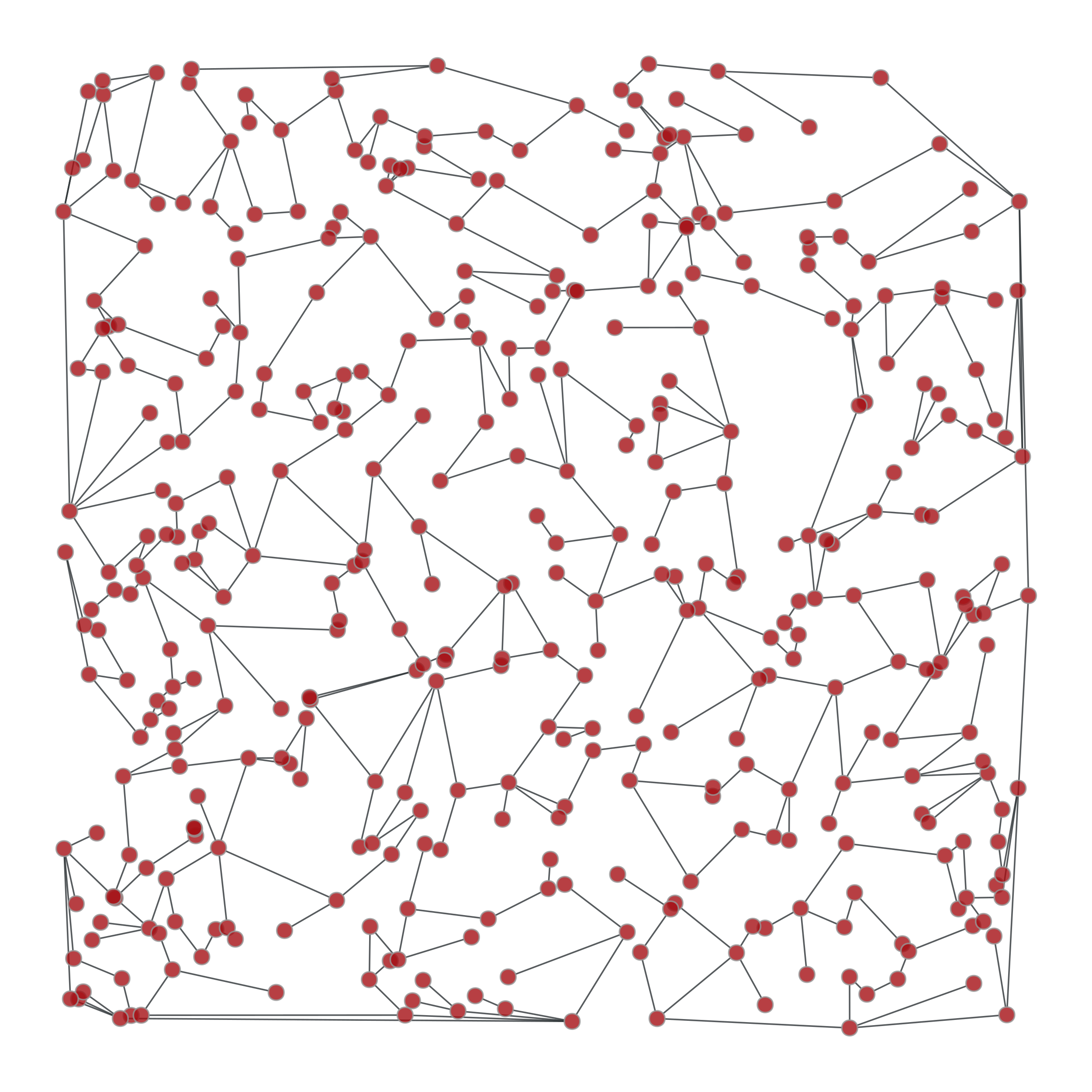
../_images/rtriang_orig.png ../_images/triang_random_span_tree.png ../_images/triang_random_span_tree2.png

Left: Original graph, Middle: A random spanning tree, Right: Another random spanning tree