graph_projection

graph_tool.generation.graph_projection(g, p, proj_props=[], props=[])

Return the projection of selected vertices on the remaning vertices.

Parameters:

gGraph

Graph to be projected.

pVertexPropertyMap

Vertex property map indicating the vertices that should be projected. A value convertible to True (i.e. a nonzero scalar value) indicates that the vertex should be projected.

proj_propslist of VertexPropertyMap objects (optional, default: [])

Vertex property maps to be included as edge property maps in the projection.

propslist of PropertyMap (optional, default: [])

Property maps to be included the projection, for nodes and edges not participating in the projection.

Returns:

pgGraph

The projected graph.

nproj_propslist of EdgePropertyMap objects

List of edge properties in the projected graph. This is only returned if proj_props is not empty.

npropslist of PropertyMap objects

List of properties in the projected graph, for nodes and edges not participating in the projection. This is only returned if props is not empty.

Notes

A vertex is projected when it’s removed from the graph, and its neighbours are connected to form a clique.

In the case of directed graphs, an edge \(u\to v\) exists in the projected graph if a path \(u\to w\to v\) exists in the original graph for a projected vertex \(w\).

The original graph does not need to be bipartite. Edges not involved in the projection are preserved.

This algorithm runs in time \(O(N + E + N_p\left<k^2\right>)\), where \(N\) and \(E\) are the number of vertices and edges, respectively, \(N_p\) is the number of vertices to be projected, and \(\left<k^2\right>\) is their average squared degree.

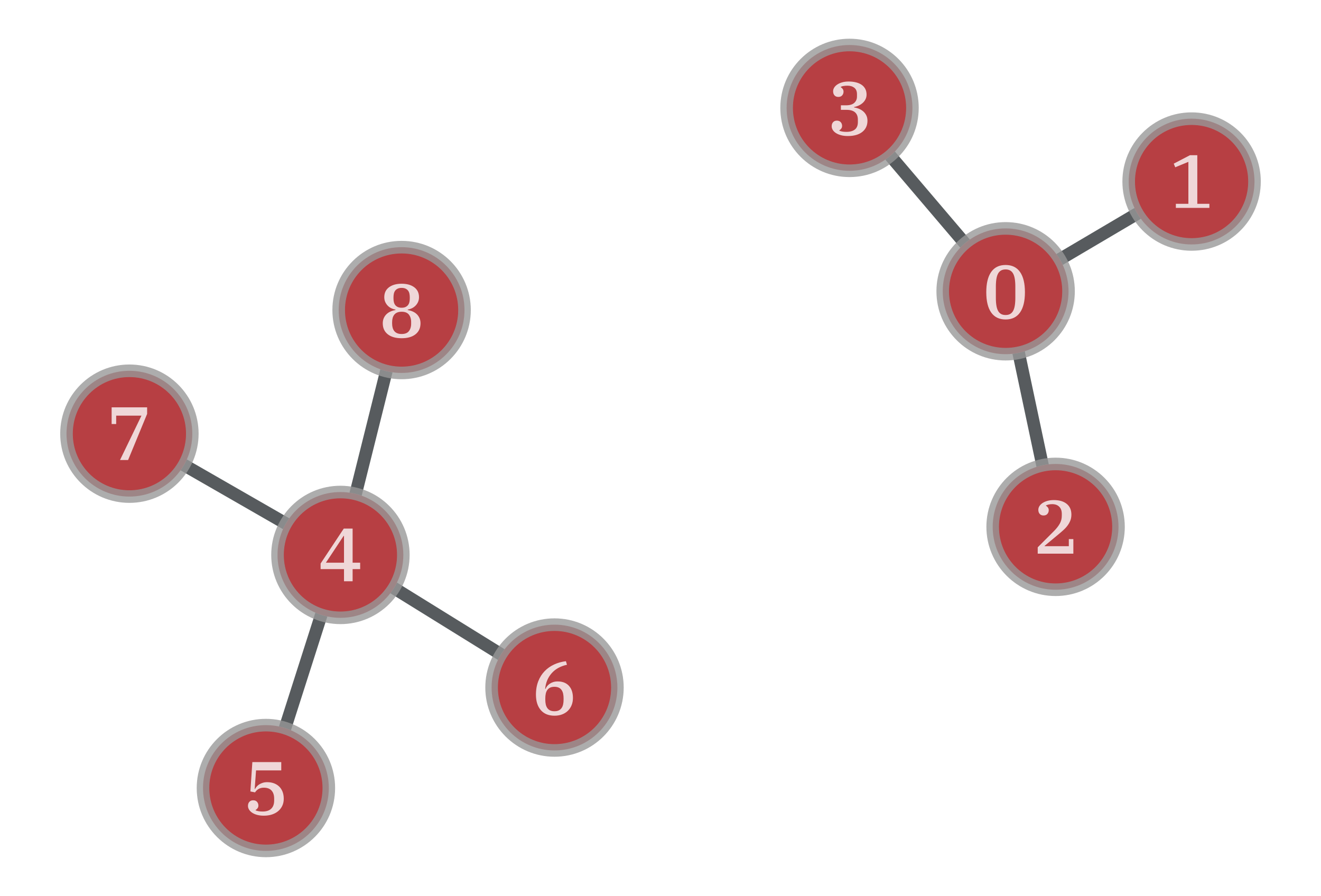
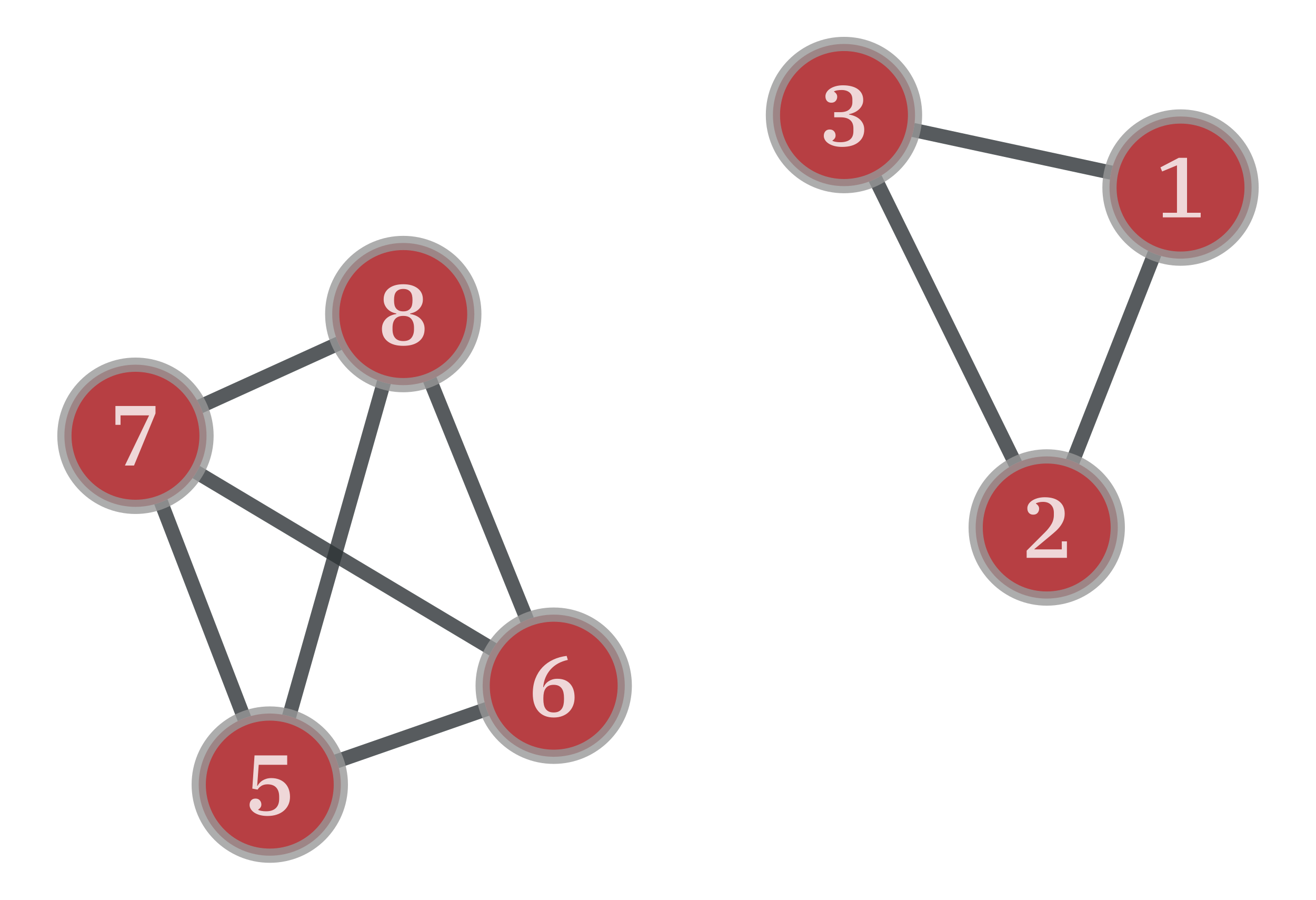
Examples

>>> g = gt.Graph({0: (1,2,3), 4: (5,6,7,8)}, directed=False)
>>> p = g.new_vp("bool", vals=[v in [0, 4] for v in g.vertices()])
>>> pos = gt.sfdp_layout(g)
>>> pg, props = gt.graph_projection(g, p, props=[g.vertex_index, pos])
>>> gt.graph_draw(g, pos=pos, vertex_text=g.vertex_index, output="bipartite_orig.pdf")
<...>
>>> gt.graph_draw(pg, pos=props[1], vertex_text=props[0], output="projection.pdf")
<...>