fruchterman_reingold_layout

graph_tool.draw.fruchterman_reingold_layout(g, weight=None, a=None, r=1.0, scale=None, circular=False, grid=True, t_range=None, n_iter=100, pos=None)

Calculate the Fruchterman-Reingold spring-block layout of the graph.

Parameters:

gGraph

Graph to be used.

weightEdgePropertyMap (optional, default: None)

An edge property map with the respective weights.

afloat (optional, default: \(V\))

Attracting force between adjacent vertices.

rfloat (optional, default: 1.0)

Repulsive force between vertices.

scalefloat (optional, default: \(\sqrt{V}\))

Total scale of the layout (either square side or radius).

circularbool (optional, default: False)

If True, the layout will have a circular shape. Otherwise the shape will be a square.

gridbool (optional, default: True)

If True, the repulsive forces will only act on vertices which are on the same site on a grid. Otherwise they will act on all vertex pairs.

t_rangetuple of floats (optional, default: (scale / 10, scale / 1000))

Temperature range used in annealing. The temperature limits the displacement at each iteration.

n_iterint (optional, default: 100)

Total number of iterations.

posVertexPropertyMap (optional, default: None)

Vector vertex property maps where the coordinates should be stored. If provided, this will also be used as the initial position of the vertices.

Returns:

posVertexPropertyMap

A vector-valued vertex property map with the coordinates of the vertices.

Notes

This algorithm is defined in [fruchterman-reingold], and has complexity \(O(\text{n-iter}\times V^2)\) if grid=False or \(O(\text{n-iter}\times (V + E))\) otherwise.

References

[fruchterman-reingold]

Fruchterman, Thomas M. J.; Reingold, Edward M. “Graph Drawing by Force-Directed Placement”. Software - Practice & Experience (Wiley) 21 (11): 1129-1164. (1991) DOI: 10.1002/spe.4380211102 [sci-hub, @tor]

Examples

>>> g = gt.price_network(300)
>>> pos = gt.fruchterman_reingold_layout(g, n_iter=1000)
>>> gt.graph_draw(g, pos=pos, output="graph-draw-fr.pdf")
<...>

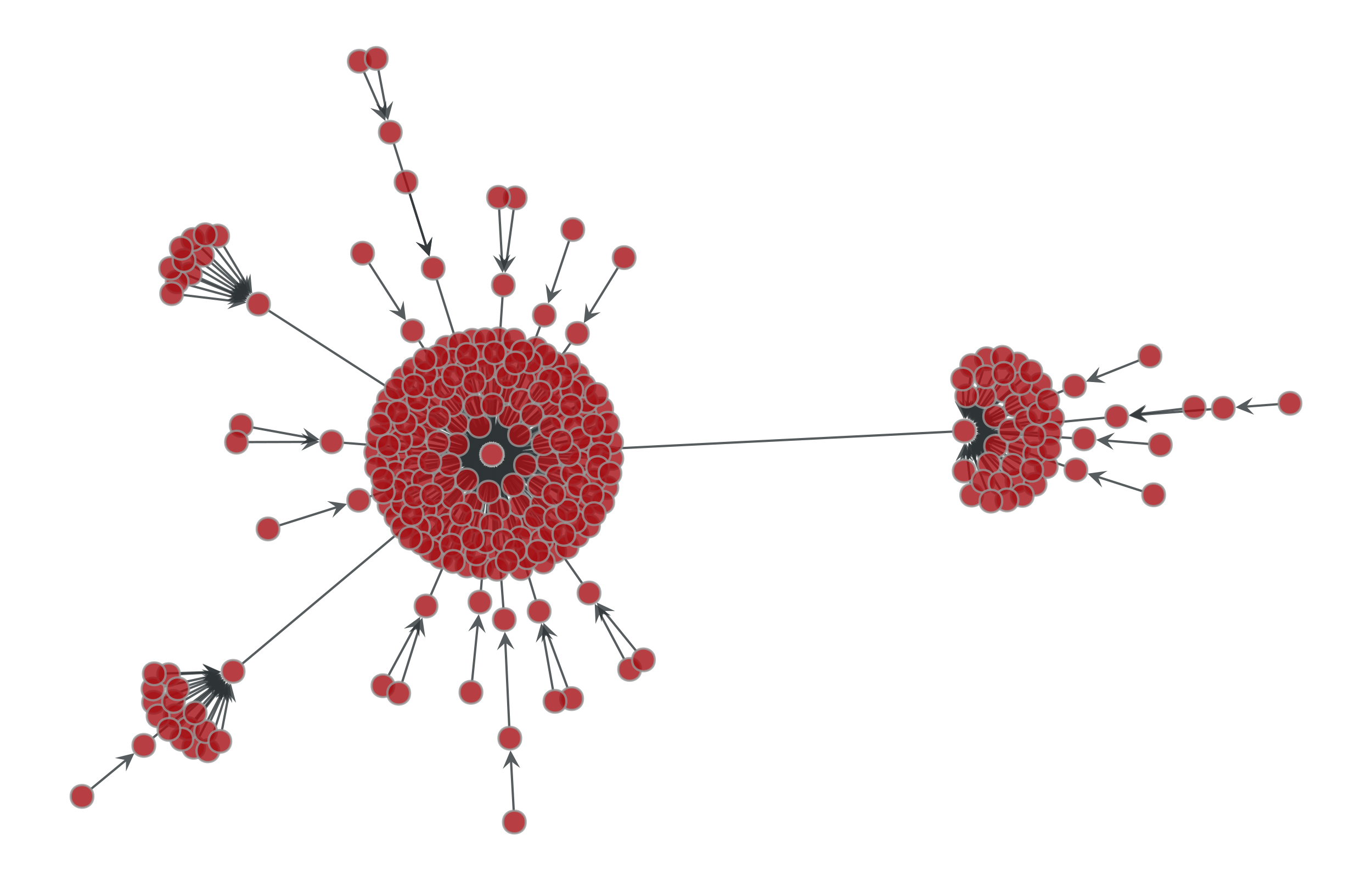
Fruchterman-Reingold layout of a Price network.