graph_merge

graph_tool.generation.graph_merge(g1, g2, eweight1=None, eweight2=None, vmap='identity', props={}, internal_props={}, in_place=False, multiset=False, diff=False, sym_diff=False, intersect=False, symmetric=False, fast_lookup=True, fast_symmetric=True, simple=False)

Merge the edges of graph g2 into g1, combining their weights, and including or excluding the edges according to the resulting weight.

Parameters:

g1Graph

Graph to be merged into.

g2Graph

Graph to be merged from.

eweight1EdgePropertyMap (optional, default: None)

If provided, this will determine the weights of the edges of graph g1. If not provided, each edge will be assumed to have unity weight.

eweight2EdgePropertyMap (optional, default: None)

If provided, this will determine the weights of the edges of graph g2. If not provided, each edge will be assumed to have unity weight.

vmapVertexPropertyMap, "identity", or None (optional, default: None)

Vertex property map owned by g2 which maps each of its vertices to vertex indices belonging to g1, in which case they are considered to be identical. Negative values mean no mapping exists, and thus both vertices in g1 and g2 will be present in the merged graph. If this argument is not provided (i.e. vmap is None), both vertex sets will be added to the merge. If vmap is g2.vertex_index, and the vertex indexes are identical in both graphs, the merge will correspond only to the edge sets. A special value of vmap == "identity" is a shortcut for vmap = g2.vertex_index.

propsdictionary with list of tuples of PropertyMap (optional, default: {})

Property maps to be considered in the merge. The key in this dictionary must be a string indicating the merge rule:

"set"

The value from g2 will be set, overwriting the value from g1.

"sum"

The value from g2 will be summed to the value from g1.

"diff"

The value from g2 will be subtracted from the value from g1.

"idx_inc"

The scalar value from g2 will be used as an index to increment the vector value from g1 by one. Alternatively, if the values from g2 are vectors, they will be interpreted as an (index, increment) pair. A negative index value means that the vector will be increased and its values shifted to the right by the absolute value of index, and the vector value at position 0 will be incremented.

"append"

The scalar value from g2 will be appended to the vector value from g1.

"concat"

The vector value from g2 will be concatenated to the vector value from g1.

The values of the dictionary must be lists, where each each element is a pair of PropertyMap objects. The first element must be a property of g1, and the second of g2. If either value is None, an new map will be created, and set to appropriately empty values.

The values of the property maps are propagated into the merged graph, and returned in a similar fashion.

internal_propsdictionary with internal property names (optional, default: {})

Internal property maps to be considered in the merge. The key in this dictionary must be a string indicating the merge rule, as documented in the props parameter.

The values must be lists of (k, name) pairs where k is one of "e", "v", "g", for edge, vertex, or graph properties, respectively, and "name" is the name of the property map.

An alternative value of "all" indicates that all property maps should be considered. E.g. props = {"set": "all"} will set all the internal property maps to the merged graph.

If an internal property map with the given name is not present in one of the graphs, an new map will be created, and set appropriately to empty values.

in_placebool (optional, default: False)

If True, graph g2 is inserted in-place into g1, which is then modified. If False, a new graph is created, and both graphs remain unmodified.

multisetbool (optional, default: False)

If True, the edges in the merged graph will form a multiset, so that a single edge that exists in both g1 and g2 becomes a parallel edge in the merged graph.

diffbool (optional, default: False)

If True the weights of the merged edges will be the weights of g1 subtracted by those of g2, otherwise they will be summed.

sym_diffbool (optional, default: False)

If True the merged edges will have as weights the absolute difference between the weights of the edges in g1 and g2.

intersectbool (optional, default: False)

If True an edge will be merged only if its weights in both g1 and g2 are nonzero.

symmetricbool (optional, default: False)

If True the edges in g1 that are not present in g2 will be removed, if they do not fulfill the merge conditions.

fast_lookupbool (optional, default: True)

If True fast edge lookup in g1 will be enabled via set_fast_edge_lookup().

fast_symmetricbool (optional, default: True)

If True and symmetric is True or simple is False, then fast edge lookup in g1 will be enabled via set_fast_edge_lookup().

simplebool (optional, default: False)

If True, it will be assumed that both g1 and g2 are simple graphs, for a faster version of the algorithm valid only in that case.

Returns:

ugGraph

The merged graph.

wEdgePropertyMap

The edge weights of the merged graph. This is only returned if eweight1 is not None.

propsdictionary with lists of PropertyMap objects

List of properties in the merged graph, index by merge type. This is only returned if props is not empty. Internal property maps are not included in this list.

See also

graph_union

Union of the edge sets between two graphs.

graph_difference

Difference of the edge sets between two graphs.

graph_sym_difference

Symmetrcic difference of the edge sets between two graphs.

graph_intersection

Intersection of the edge sets between two graphs.

condensation_graph

Obtain the condensation graph.

Notes

The algorithm runs in time \(O(N_1 + N_2 + E_1 + E_2)\), where \(N_1\), \(N_2\), \(E_1\), and \(E_2\) are the number of vertices and edges, for g1 and g2, respectively.

If symmetric is False, in_place is True, and either multiset is True or both get_fast_edge_lookup() and get_fast_edge_removal() returns True for g1, the algorithmic complexity becomes instead \(O(N_2 + E_2)\). In this situation it becomes efficient to merge a relatively small graph g2 into an arbitrarily large graph g1.

Parallel implementation.

If enabled during compilation, this algorithm will run in parallel using OpenMP. See the parallel algorithms section for information about how to control several aspects of parallelization.

Examples

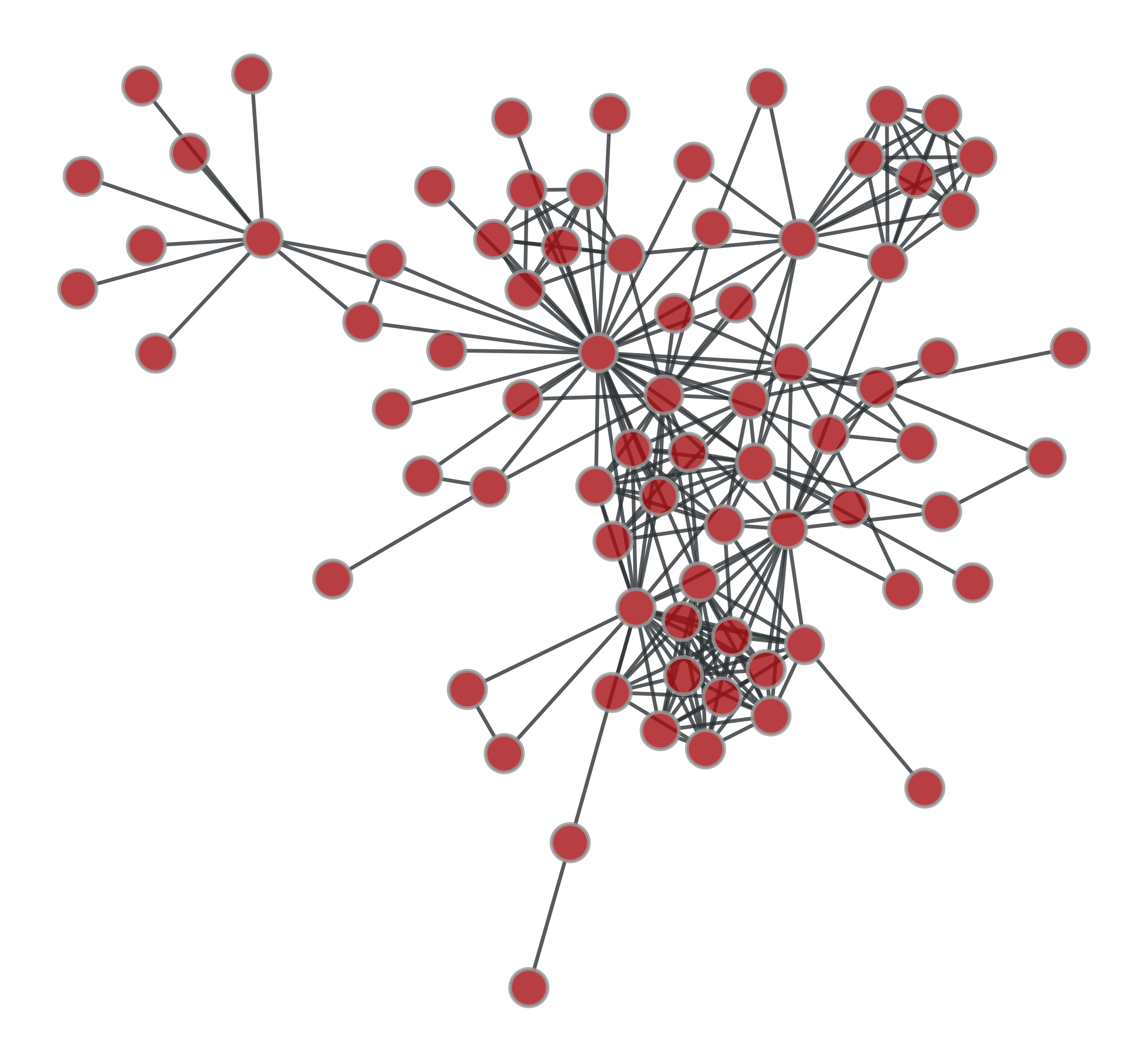
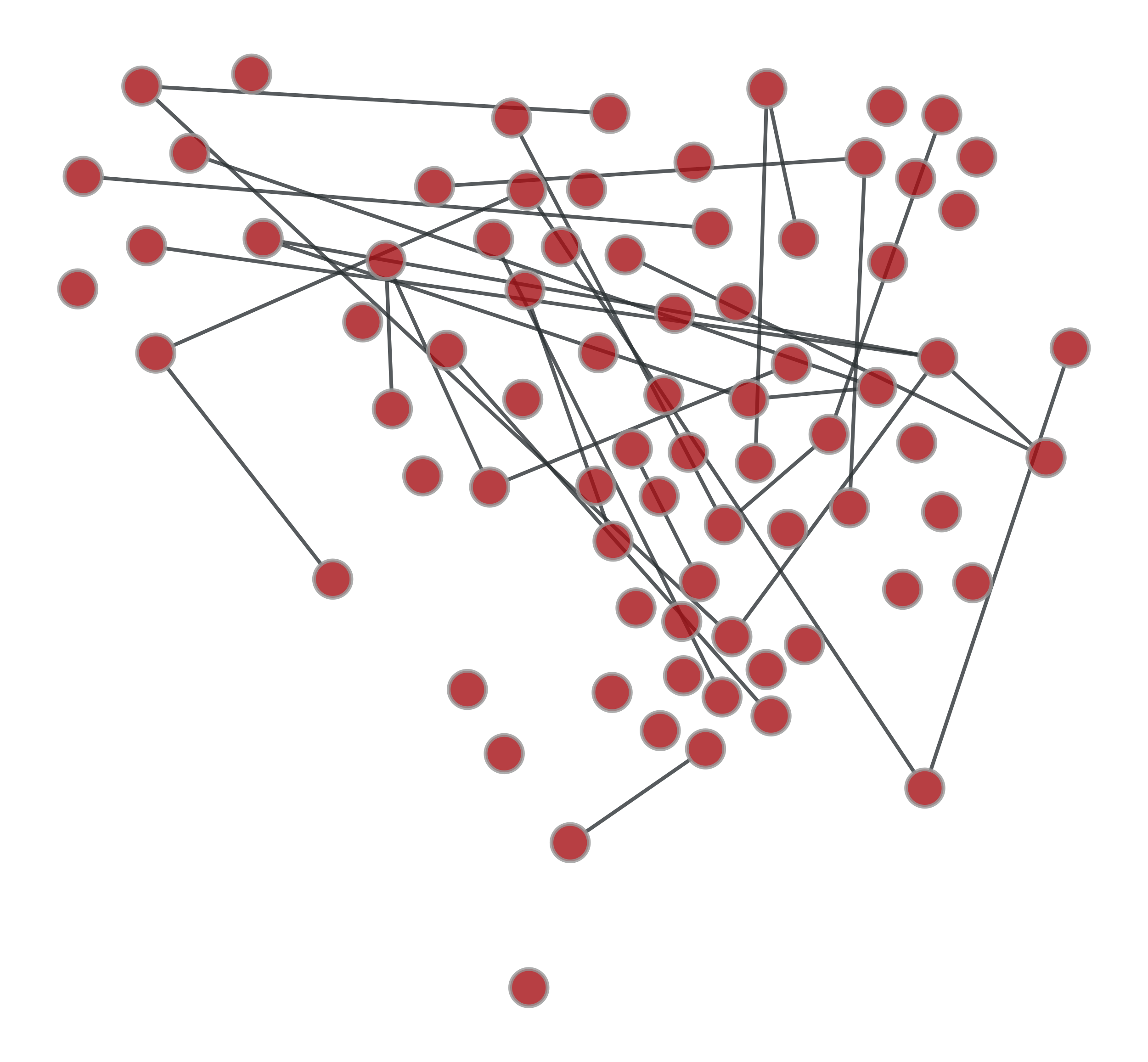
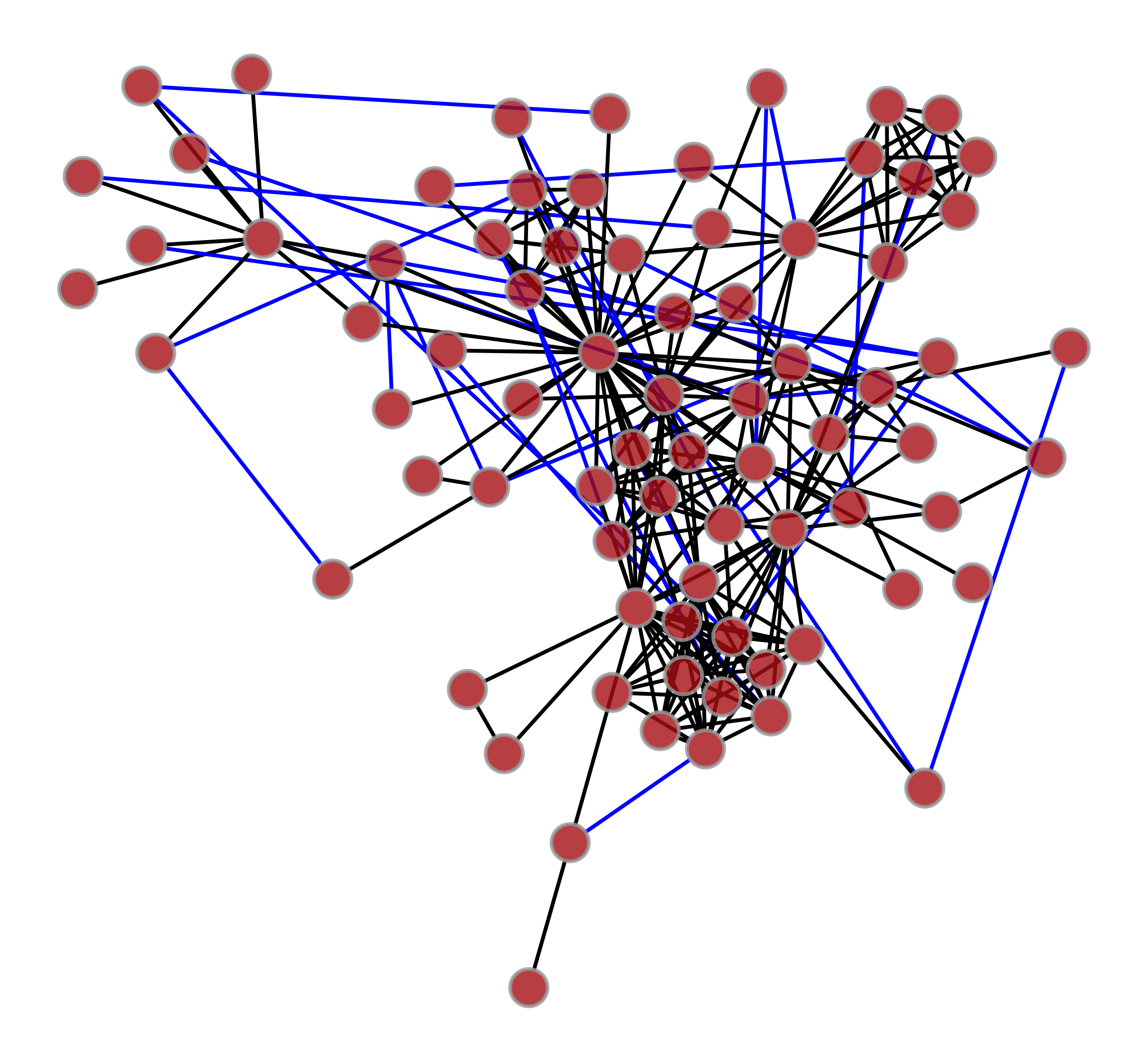
>>> g1 = gt.collection.ns["lesmis"]
>>> g2 = gt.random_graph(77, lambda: np.random.poisson(1), directed=False, model="erdos")
>>> label1 = g1.new_ep("int", val=0)
>>> label2 = g2.new_ep("int", val=1)
>>> u, ps = gt.graph_merge(g1, g2, props={"set": [(label1, label2)]})
>>> label = ps["set"][0]
>>> gt.graph_draw(g1, pos=g1.vp._pos, output="g1.pdf")
<...>
>>> gt.graph_draw(g2, pos=g1.vp._pos, output="g2.pdf")
<...>
>>> gt.graph_draw(u, pos=u.own_property(g1.vp._pos),
...               edge_color=label.t(lambda x: "black" if x == 0 else "blue",
...                                   value_type="string", no_array=True),
...               edge_pen_width=2, output="gmerge.pdf")
<...>