Quick start guide#

The graph_tool module provides a Graph class and several algorithms that operate on it. The internals of this class, and of most algorithms, are written in C++ for performance, using the Boost Graph Library.

The module must be of course imported before it can be used. The package is subdivided into several sub-modules. To import everything from all of them, one can do:

>>> from graph_tool.all import *

In the following, it will always be assumed that the previous line was run.

Creating graphs#

An empty graph can be created by instantiating a Graph class:

>>> g = Graph()

By default, newly created graphs are always directed. To construct undirected graphs, one must pass a value to the directed parameter:

>>> ug = Graph(directed=False)

A graph can always be switched on-the-fly from directed to undirected (and vice versa), with the set_directed() method. The “directedness” of the graph can be queried with the is_directed() method:

>>> ug = Graph()
>>> ug.set_directed(False)
>>> assert ug.is_directed() == False

Once a graph is created, it can be populated with vertices and edges. A vertex can be added with the add_vertex() method, which returns an instance of a Vertex class, also called a vertex descriptor. For instance, the following code creates two vertices, and returns vertex descriptors stored in the variables v1 and v2.

>>> v1 = g.add_vertex()
>>> v2 = g.add_vertex()

Edges can be added in an analogous manner, by calling the add_edge() method, which returns an edge descriptor (an instance of the Edge class):

>>> e = g.add_edge(v1, v2)

The above code creates a directed edge from v1 to v2.

A graph can also be created by providing another graph, in which case the entire graph (and its internal property maps, see Property maps) is copied:

>>> g2 = Graph(g)                 # g2 is a copy of g

Above, g2 is a “deep” copy of g, i.e. any modification of g2 will not affect g.

Note

Graph visualization in graph-tool can be interactive! When the output parameter of graph_draw() is omitted, instead of saving to a file, the function opens an interactive window. From there, the user can zoom in or out, rotate the graph, select and move individual nodes or node selections. See GraphWidget() for documentation on the interactive interface.

If you are using a Jupyter notebook, the graphs are drawn inline if output is omitted. If an interactive window is desired instead, the option inline = False should be passed.

We can visualize the graph we created so far with the graph_draw() function.

>>> graph_draw(g, vertex_text=g.vertex_index, output="two-nodes.svg")
<...>

_images/two-nodes.svg — A simple directed graph with two vertices and one edge, created by the commands above.#

We can add attributes to the nodes and edges of our graph via property maps. For example, suppose we want to add an edge weight and node color to our graph we have first to create two PropertyMap objects as such:

>>> eweight = g.new_ep("double")    # creates an EdgePropertyMap of type double
>>> vcolor = g.new_vp("string")     # creates a VertexPropertyMap of type string

And now we set their values for each vertex and edge:

>>> eweight[e] = 25.3
>>> vcolor[v1] = "#1c71d8"
>>> vcolor[v2] = "#2ec27e"

Property maps can then be used in many graph-tool functions to set node and edge properties, for example:

>>> graph_draw(g, vertex_text=g.vertex_index, vertex_fill_color=vcolor,
...            edge_pen_width=eweight, output="two-nodes-color.svg")
<...>

_images/two-nodes-color.svg — The same graph as before, but with edge width and node color specified by property maps.#

Property maps are discussed in more detail in the section Property maps below.

Adding many edges and vertices at once#

Note

The vertex values passed to the constructor need to be integers per default, but arbitrary objects can be passed as well if the option hashed = True is passed. In this case, the mapping of vertex descriptors to vertex ids is obtained via an internal VertexPropertyMap called "ids". E.g. in the example above we have

>>> print(g.vp.ids[0])
foo

See Property maps below for more details.

It is also possible to add many edges and vertices at once when the graph is created. For example, it is possible to construct graphs directly from a list of edges, e.g.

>>> g = Graph([('foo', 'bar'), ('gnu', 'gnat')], hashed=True)

which is just a convenience shortcut to creating an empty graph and calling add_edge_list() afterward, as we will discuss below.

Edge properties can also be initialized together with the edges by using tuples (source, target, property_1, property_2, ...), e.g.

>>> g = Graph([('foo', 'bar', .5, 1), ('gnu', 'gnat', .78, 2)], hashed=True,
...           eprops=[('weight', 'double'), ('time', 'int')])

The eprops parameter lists the name and value types of the properties, which are used to create internal property maps with the value encountered (see Property maps below for more details).

It is possible also to pass an adjacency list to construct a graph, which is a dictionary of out-neighbors for every vertex key:

>>> g = Graph({0: [2, 3], 1: [4], 3: [4, 5], 6: []})

We can also easily construct graphs from adjacency matrices. They need only to be converted to a sparse scipy matrix (i.e. a subclass of scipy.sparse.sparray or scipy.sparse.spmatrix) and passed to the constructor, e.g.:

>>> m = np.array([[0, 1, 0],
...               [0, 0, 1],
...               [0, 1, 0]])
>>> g = Graph(scipy.sparse.lil_matrix(m))

The nonzero entries of the matrix are stored as an edge property map named "weight" (see Property maps below for more details), e.g.

>>> m = np.array([[0, 1.2, 0],
...               [0, 0, 10],
...               [0, 7, 0]])
>>> g = Graph(scipy.sparse.lil_matrix(m))
>>> print(g.ep.weight.a)
[ 1.2 10.   7. ]

For undirected graphs (i.e. the option directed = False is given) only the upper triangular portion of the passed matrix will be considered, and the remaining entries will be ignored.

We can also add many edges at once after the graph has been created using the add_edge_list() method. It accepts any iterable of (source, target) pairs, and automatically adds any new vertex seen:

>>> g.add_edge_list([(0, 1), (2, 3)])

Note

As above, if hashed = True is passed, the function add_edge_list() returns a VertexPropertyMap object that maps vertex descriptors to their id values in the list. See Property maps below.

The vertex values passed to add_edge_list() need to be integers per default, but arbitrary objects can be passed as well if the option hashed = True is passed, e.g. for string values:

>>> g.add_edge_list([('foo', 'bar'), ('gnu', 'gnat')], hashed=True,
...                 hash_type="string")
<...>

or for arbitrary (hashable) Python objects:

>>> g.add_edge_list([((2, 3), 'foo'), (3, 42.3)], hashed=True,
...                 hash_type="object")
<...>

Manipulating graphs#

With vertex and edge descriptors at hand, one can examine and manipulate the graph in an arbitrary manner. For instance, in order to obtain the out-degree of a vertex, we can simply call the out_degree() method:

>>> g = Graph()
>>> v1 = g.add_vertex()
>>> v2 = g.add_vertex()
>>> e = g.add_edge(v1, v2)
>>> print(v1.out_degree())
1

Note

For undirected graphs, the “out-degree” is synonym for degree, and in this case the in-degree of a vertex is always zero.

Analogously, we could have used the in_degree() method to query the in-degree.

Edge descriptors have two useful methods, source() and target(), which return the source and target vertex of an edge, respectively.

>>> print(e.source(), e.target())
0 1

We can also directly convert an edge to a tuple of vertices, to the same effect:

>>> u, v = e
>>> print(u, v)
0 1

The add_vertex() method also accepts an optional parameter which specifies the number of additional vertices to create. If this value is greater than 1, it returns an iterator on the added vertex descriptors:

>>> vlist = g.add_vertex(10)
>>> print(len(list(vlist)))
10

Each vertex in a graph has a unique index, which is *always* between \(0\) and \(N-1\), where \(N\) is the number of vertices. This index can be obtained by using the vertex_index attribute of the graph (which is a property map, see Property maps), or by converting the vertex descriptor to an int.

>>> v = g.add_vertex()
>>> print(g.vertex_index[v])
12
>>> print(int(v))
12

Edges and vertices can also be removed at any time with the remove_vertex() and remove_edge() methods,

>>> g.remove_edge(e)                               # e no longer exists
>>> g.remove_vertex(v2)                # the second vertex is also gone

When removing edges, it is important to keep in mind some performance considerations:

Warning

Because of the contiguous indexing, removing a vertex with an index smaller than \(N-1\) will invalidate either the last (fast == True) or all (fast == False) descriptors pointing to vertices with higher index.

As a consequence, if more than one vertex is to be removed at a given time, they should always be removed in decreasing index order:

# 'vs' is a list of
# vertex descriptors
vs = sorted(vs)
vs = reversed(vs)
for v in vs:
    g.remove_vertex(v)

Alternatively (and preferably), a list (or any iterable) may be passed directly as the vertex parameter of the remove_vertex() function, and the above is performed internally (in C++).

Note that property map values (see Property maps) are unaffected by the index changes due to vertex removal, as they are modified accordingly by the library.

Note

Removing a vertex is typically an \(O(N)\) operation. The vertices are internally stored in a STL vector, so removing an element somewhere in the middle of the list requires the shifting of the rest of the list. Thus, fast \(O(1)\) removals are only possible if one can guarantee that only vertices in the end of the list are removed (the ones last added to the graph), or if the relative vertex ordering is invalidated. The latter behavior can be achieved by passing the option fast = True, to remove_vertex(), which causes the vertex being deleted to be ‘swapped’ with the last vertex (i.e. with the largest index), which, in turn, will inherit the index of the vertex being deleted.

Removing an edge is an \(O(k_{s} + k_{t})\) operation, where \(k_{s}\) is the out-degree of the source vertex, and \(k_{t}\) is the in-degree of the target vertex. This can be made faster by setting set_fast_edge_removal() to True, in which case it becomes \(O(1)\), at the expense of additional data of size \(O(E)\).

No edge descriptors are ever invalidated after edge removal, with the exception of the edge itself that is being removed.

Since vertices are uniquely identifiable by their indices, there is no need to keep the vertex descriptor lying around to access them at a later point. If we know its index, we can obtain the descriptor of a vertex with a given index using the vertex() method,

>>> v = g.vertex(8)

which takes an index, and returns a vertex descriptor. Edges cannot be directly obtained by its index, but if the source and target vertices of a given edge are known, it can be retrieved with the edge() method

>>> g.add_edge(g.vertex(2), g.vertex(3))
<...>
>>> e = g.edge(2, 3)

Another way to obtain edge or vertex descriptors is to iterate through them, as described in section Iterating over vertices and edges. This is in fact the most useful way of obtaining vertex and edge descriptors.

Like vertices, edges also have unique indices, which are given by the edge_index property:

>>> e = g.add_edge(g.vertex(0), g.vertex(1))
>>> print(g.edge_index[e])
1

Differently from vertices, edge indices do not necessarily conform to any specific range. If no edges are ever removed, the indices will be in the range \([0, E-1]\), where \(E\) is the number of edges, and edges added earlier have lower indices. However if an edge is removed, its index will be “vacant”, and the remaining indices will be left unmodified, and thus will not all lie in the range \([0, E-1]\). If a new edge is added, it will reuse old indices, in an increasing order.

Iterating over vertices and edges#

Algorithms must often iterate through vertices, edges, out-edges of a vertex, etc. The Graph and Vertex classes provide different types of iterators for doing so. The iterators always point to edge or vertex descriptors.

Iterating over all vertices or edges#

In order to iterate through all the vertices or edges of a graph, the vertices() and edges() methods should be used:

for v in g.vertices():
    print(v)
for e in g.edges():
    print(e)

The code above will print the vertices and edges of the graph in the order they are found.

Iterating over the neighborhood of a vertex#

Warning

You should never remove vertex or edge descriptors when iterating over them, since this invalidates the iterators. If you plan to remove vertices or edges during iteration, you must first store them somewhere (such as in a list) and remove them only after no iterator is being used. Removal during iteration will cause bad things to happen.

The out- and in-edges of a vertex, as well as the out- and in-neighbors can be iterated through with the out_edges(), in_edges(), out_neighbors() and in_neighbors() methods, respectively.

for v in g.vertices():
   for e in v.out_edges():
       print(e)
   for w in v.out_neighbors():
       print(w)

   # the edge and neighbors order always match
   for e, w in zip(v.out_edges(), v.out_neighbors()):
       assert e.target() == w

The code above will print the out-edges and out-neighbors of all vertices in the graph.

Property maps#

Property maps are a way of associating additional information to the vertices, edges, or to the graph itself. There are thus three types of property maps: vertex, edge, and graph. They are handled by the classes VertexPropertyMap, EdgePropertyMap, and GraphPropertyMap. Each created property map has an associated value type, which must be chosen from the predefined set:

Type name	Alias
`bool`	`uint8_t`
`int16_t`	`short`
`int32_t`	`int`
`int64_t`	`long`, `long long`
`double`	`float`
`long double`
`string`
`vector<bool>`	`vector<uint8_t>`
`vector<int16_t>`	`vector<short>`
`vector<int32_t>`	`vector<int>`
`vector<int64_t>`	`vector<long>`, `vector<long long>`
`vector<double>`	`vector<float>`
`vector<long double>`
`vector<string>`
`python::object`	`object`

New property maps can be created for a given graph by calling one of the methods new_vertex_property() (alias new_vp()), new_edge_property() (alias new_ep()), or new_graph_property() (alias new_gp()), for each map type. The values are then accessed by vertex or edge descriptors, or the graph itself, as such:

from numpy.random import randint

g = Graph()
g.add_vertex(100)

# insert some random links
for s,t in zip(randint(0, 100, 100), randint(0, 100, 100)):
    g.add_edge(g.vertex(s), g.vertex(t))

vprop = g.new_vertex_property("double")              # Double-precision floating point
v = g.vertex(10)
vprop[v] = 3.1416

vprop2 = g.new_vertex_property("vector<int>")        # Vector of ints
v = g.vertex(40)
vprop2[v] = [1, 3, 42, 54]

eprop = g.new_edge_property("object")                # Arbitrary Python object.
e = g.edges().next()
eprop[e] = {"foo": "bar", "gnu": 42}                 # In this case, a dict.

gprop = g.new_graph_property("bool")                 # Boolean
gprop[g] = True

It is possible also to access vertex property maps directly by vertex indices:

>>> print(vprop[10])
3.1416

Warning

The following lines are equivalent:

eprop[(30, 40)]
eprop[g.edge(30, 40)]

Which means that indexing via (source, target) pairs is slower than via edge descriptors, since the function edge() needs to be called first.

And likewise we can access edge descriptors via (source, target) pairs:

>>> g.add_edge(30, 40)
<...>
>>> eprop[(30, 40)] = "gnat"

We can also iterate through the property map values directly, i.e.

>>> print(list(vprop)[:10])
[0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0]

Property maps with scalar value types can also be accessed as a numpy.ndarray, with the get_array() method, or the a attribute, e.g.,

from numpy.random import random

# this assigns random values to the vertex properties
vprop.get_array()[:] = random(g.num_vertices())

# or more conveniently (this is equivalent to the above)
vprop.a = random(g.num_vertices())

Array interface for filtered graphs

For filtered graphs (see Graph filtering below), it’s possible to get arrays that only point to the nodes and edges that are not filtered out via the fa and ma attributes instead.

Transformations#

We usually want to apply transformations to the values of property maps. This can be achieved via iteration (see Iterating over vertices and edges), but since this is a such a common operation, there’s a more convenient way to do this via the transform() method (or is shorter alias t()), which takes a function and returns a copy of the property map with the function applied to its values:

# Vertex property map with random values in the range [-.5, .5]
rand = g.new_vp("double", vals=random(g.num_vertices()) - .5)

# The following returns a copy of `rand` but containing only the absolute values
m = rand.t(abs)

Tip

Transformations are particularly useful to pass temporary properties to functions, e.g.

erand = g.new_ep("double", vals=random(g.num_edges()) - .5)
pos = sfdp_layout(g, eweight=erand.t(abs))

Internal property maps#

Any created property map can be made “internal” to the corresponding graph. This means that it will be copied and saved to a file together with the graph. Properties are internalized by including them in the graph’s dictionary-like attributes vertex_properties, edge_properties or graph_properties (or their aliases, vp, ep or gp, respectively). When inserted in the graph, the property maps must have an unique name (between those of the same type):

>>> eprop = g.new_edge_property("string")
>>> g.ep["some name"] = eprop
>>> g.list_properties()
some name      (edge)    (type: string)

Internal graph property maps behave slightly differently. Instead of returning the property map object, the value itself is returned from the dictionaries:

>>> gprop = g.new_graph_property("int")
>>> g.gp["foo"] = gprop                 # this sets the actual property map
>>> g.gp["foo"] = 42                    # this sets its value
>>> print(g.gp["foo"])
42
>>> del g.gp["foo"]                     # the property map entry is deleted from the dictionary

For convenience, the internal property maps can also be accessed via attributes:

>>> vprop = g.new_vertex_property("double")
>>> g.vp.foo = vprop                    # equivalent to g.vp["foo"] = vprop
>>> v = g.vertex(0)
>>> g.vp.foo[v] = 3.14
>>> print(g.vp.foo[v])
3.14

Graph I/O#

Graphs can be saved and loaded in four formats: graphml, dot, gml and a custom binary format gt (see The gt file format).

Warning

The binary format gt and the text-based graphml are the preferred formats, since they are by far the most complete. Both these formats are equally complete, but the gt format is faster and requires less storage.

The dot and gml formats are fully supported, but since they contain no precise type information, all properties are read as strings (or also as double, in the case of gml), and must be converted by hand to the desired type. Therefore you should always use either gt or graphml, since they implement an exact bit-for-bit representation of all supported Property maps types, except when interfacing with other software, or existing data, which uses dot or gml.

Note

Graph classes can also be pickled with the pickle module.

A graph can be saved or loaded to a file with the save and load methods, which take either a file name or a file-like object. A graph can also be loaded from disc with the load_graph() function, as such:

g = Graph()
#  ... fill the graph ...
g.save("my_graph.gt.gz")
g2 = load_graph("my_graph.gt.gz")
# g and g2 should be identical copies of each other

Graph filtering#

Note

It is important to emphasize that the filtering functionality does not add any performance overhead when the graph is not being filtered. In this case, the algorithms run just as fast as if the filtering functionality didn’t exist.

One of the unique features of graph-tool is the “on-the-fly” filtering of edges and/or vertices. Filtering means the temporary masking of vertices/edges, which are in fact not really removed, and can be easily recovered.

Ther are two different ways to enable graph filtering: via graph views or inplace filtering, which are covered in the following.

Graph views#

It is often desired to work with filtered and unfiltered graphs simultaneously, or to temporarily create a filtered version of graph for some specific task. For these purposes, graph-tool provides a GraphView class, which represents a filtered “view” of a graph, and behaves as an independent graph object, which shares the underlying data with the original graph. Graph views are constructed by instantiating a GraphView class, and passing a graph object which is supposed to be filtered, together with the desired filter parameters. For example, to create a directed view of an undirected graph g above, one could do:

>>> ug = GraphView(g, directed=True)
>>> ug.is_directed()
True

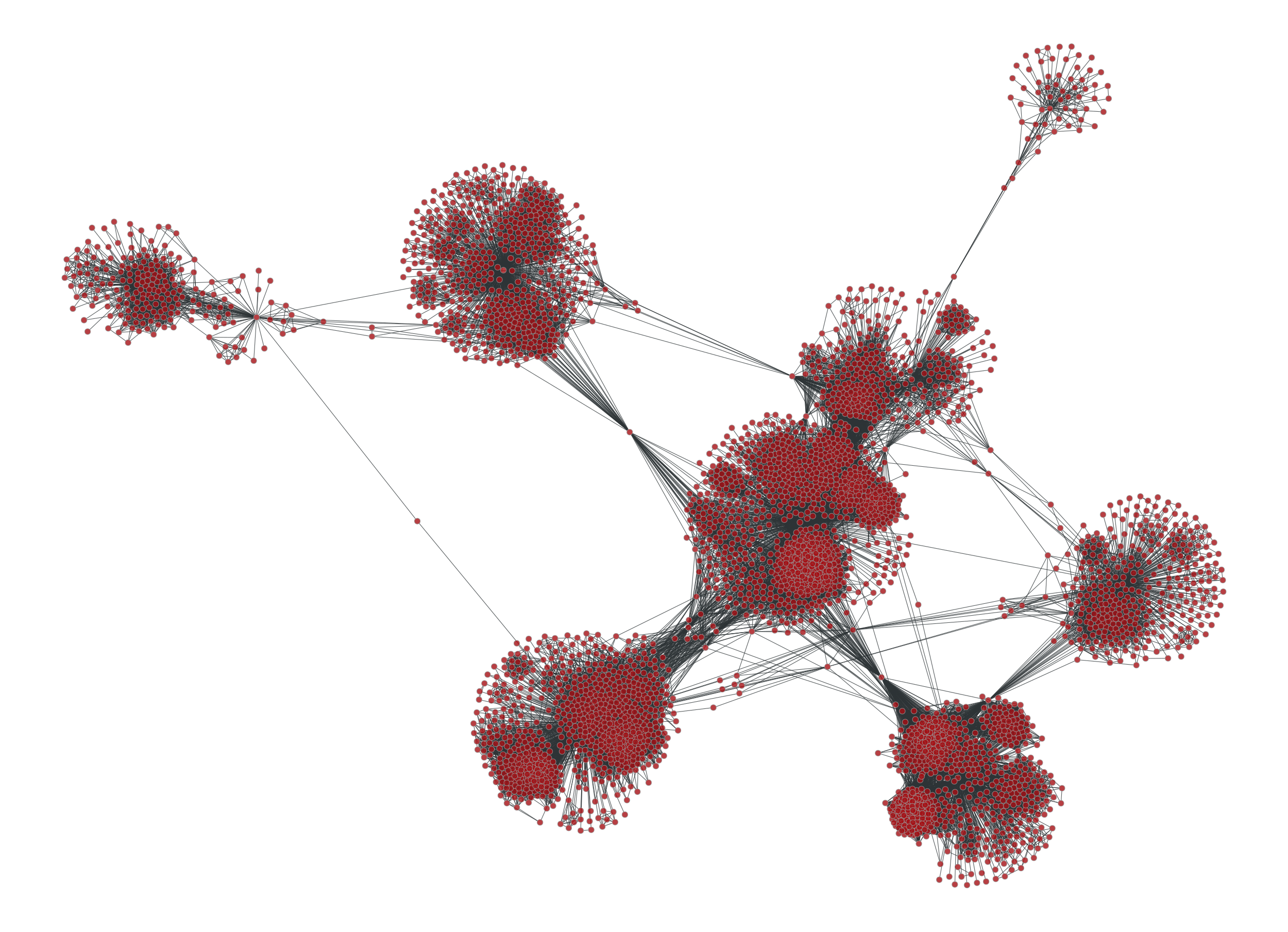
Graph views also provide a direct and convenient approach to vertex/edge filtering. Let us consider the facebook friendship graph we used before and the betweeness centrality values:

>>> g = collection.ns["ego_social/facebook_combined"]
>>> vb, eb = betweenness(g)

Let us suppose we would like to see how the graph would look like if some of the edges with higher betweeness values were removed. We can do this by a GraphView object and passing the efilt paramter:

>>> u = GraphView(g, vfilt=eb.fa < 1e-6)

Note

GraphView objects behave exactly like regular Graph objects. In fact, GraphView is a subclass of Graph. The only difference is that a GraphView object shares its internal data with its parent Graph class. Therefore, if the original Graph object is modified, this modification will be reflected immediately in the GraphView object, and vice versa.

Since GraphView is a derived class from Graph, and its instances are accepted as regular graphs by every function of the library. Graph views are “first class citizens” in graph-tool.

If we visualize the graph we can see it now has been broken up in many components:

>>> graph_draw(u, pos=g.vp._pos, output="facebook-filtered.pdf")
<...>

_images/facebook-filtered.png — Facebook friendship network with edges with a betweeness centrality value above \(10^{-6}\) filtered out.#

Note however that no copy of the original graph was done, and no edge has been in fact removed. If we inspect the original graph g in the example above, it will be intact.

In the example above, we passed a boolean array as the efilt, but we could have passed also a boolean property map, a function that takes an edge as single parameter, and returns True if the edge should be kept and False otherwise. For instance, the above could be equivalently achieved as:

>>> u = GraphView(g, efilt=lambda e: eb[e] < 1e-6)

But note however that would be slower, since it would involve one function call per edge in the graph.

Vertices can also be filtered in an entirerly analogous fashion using the vfilt paramter.

Composing graph views#

Since graph views behave like regular graphs, one can just as easily create graph views of graph views. This provides a convenient way of composing filters. For instance, suppose we wanto to isolate the minimum spanning tree of all vertices of agraph above which have a degree larger than four:

>>> g, pos = triangulation(random((500, 2)) * 4, type="delaunay")
>>> u = GraphView(g, vfilt=lambda v: v.out_degree() > 4)
>>> tree = min_spanning_tree(u)
>>> u = GraphView(u, efilt=tree)

The resulting graph view can be used and visualized as normal:

>>> bv, be = betweenness(u)
>>> be.a /= be.a.max() / 5
>>> graph_draw(u, pos=pos, vertex_fill_color=bv,
...            edge_pen_width=be, output="mst-view.svg")
<...>

_images/mst-view.svg — A composed view, obtained as the minimum spanning tree of all vertices in the graph which have a degree larger than four. The edge thickness indicates the betweeness values, as well as the node colors.#

In-place graph filtering#

It is possible also to filter graphs “in-place”, i.e. without creating an additional object. To achieve this, vertices or edges which are to be filtered should be marked with a PropertyMap with value type bool, and then set with set_vertex_filter() or set_edge_filter() methods. By default, vertex or edges with value “1” are kept in the graphs, and those with value “0” are filtered out. This behaviour can be modified with the inverted parameter of the respective functions. All manipulation functions and algorithms will work as if the marked edges or vertices were removed from the graph, with minimum overhead.

For example, to reproduce the same example as before for the facebook graph we could have done:

>>> g = collection.ns["ego_social/facebook_combined"]
>>> vb, eb = betweenness(g)
>>> mask = g.new_ep("bool", vals = eb.fa < 1e-5)
>>> g.set_edge_filter(mask)

The mask property map has a bool type, with value 1 if the edge belongs to the tree, and 0 otherwise.

Everything should work transparently on the filtered graph, simply as if the masked edges were removed.

The original graph can be recovered by setting the edge filter to None.

g.set_edge_filter(None)

Everything works in analogous fashion with vertex filtering.

Additionally, the graph can also have its edges reversed with the set_reversed() method. This is also an \(O(1)\) operation, which does not really modify the graph.

As mentioned previously, the directedness of the graph can also be changed “on-the-fly” with the set_directed() method.

Advanced iteration#

Faster iteration over vertices and edges without descriptors#

The mode of iteration considered above is convenient, but requires the creation of vertex and edge descriptor objects, which incurs a performance overhead. A faster approach involves the use of the methods iter_vertices(), iter_edges(), iter_out_edges(), iter_in_edges(), iter_all_edges(), iter_out_neighbors(), iter_in_neighbors(), iter_all_neighbors(), which return vertex indices and pairs thereof, instead of descriptors objects, to specify vertex and edges, respectively.

For example, for the graph:

g = Graph([(0, 1), (2, 3), (2, 4)])

we have

for v in g.iter_vertices():
    print(v)
for e in g.iter_edges():
    print(e)

which yields

0
1
2
3
4
[0, 1]
[2, 3]
[2, 4]

and likewise for the iteration over the neighborhood of a vertex:

for v in g.iter_vertices():
   for e in g.iter_out_edges(v):
       print(e)
   for w in g.iter_out_neighbors(v):
       print(w)

Even faster, “loopless” iteration over vertices and edges using arrays#

While more convenient, looping over the graph as described in the previous sections are not quite the most efficient approaches to operate on graphs. This is because the loops are performed in pure Python, thus undermining the main feature of the library, which is the offloading of loops from Python to C++. Following the numpy philosophy, graph_tool also provides an array-based interface that avoids loops in Python. This is done with the get_vertices(), get_edges(), get_out_edges(), get_in_edges(), get_all_edges(), get_out_neighbors(), get_in_neighbors(), get_all_neighbors(), get_out_degrees(), get_in_degrees() and get_total_degrees() methods, which return numpy.ndarray instances instead of iterators.

For example, using this interface we can get the out-degree of each node via:

print(g.get_out_degrees(g.get_vertices()))

[1 0 2 0 0]

or the sum of the product of the in and out-degrees of the endpoints of each edge with:

edges = g.get_edges()
in_degs = g.get_in_degrees(g.get_vertices())
out_degs = g.get_out_degrees(g.get_vertices())
print((out_degs[edges[:,0]] * in_degs[edges[:,1]]).sum())

Quick start guide

Contents

Quick start guide#

Creating graphs#

Adding many edges and vertices at once#

Manipulating graphs#

Iterating over vertices and edges#

Iterating over all vertices or edges#

Iterating over the neighborhood of a vertex#

Example analysis: an online social network#

Property maps#

Transformations#

Internal property maps#

Graph I/O#

Graph filtering#

Graph views#

Composing graph views#

In-place graph filtering#

Advanced iteration#

Faster iteration over vertices and edges without descriptors#

Even faster, “loopless” iteration over vertices and edges using arrays#